题目内容
在△ABC中,∠BAC=90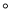 ,AB=AC.点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,使
,AB=AC.点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,使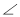 DAE=90
DAE=90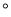 ,连结CE.
,连结CE.
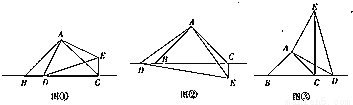
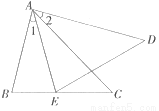
探究:如图①,当点D在线段BC上时,证明BC=CE+CD.
应用:在探究的条件下,若AB=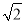 ,CD=1,则△DCE的周长为_______.
,CD=1,则△DCE的周长为_______.
拓展:(1)如图②,当点D在线段CB的延长线上时,BC、CD、CE之间的数量关系为_______.
(2)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为_______.
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目


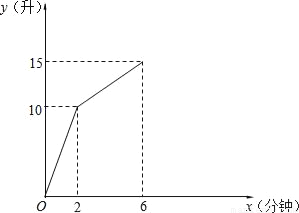
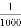 ,说明每买1 000张彩票,一定有一张中奖
,说明每买1 000张彩票,一定有一张中奖
 B.
B.  C.
C.  D.
D. 