题目内容
【题目】在平面直角坐标系![]() 中,对“隔离直线”给出如下定义:点
中,对“隔离直线”给出如下定义:点![]() 是图形
是图形![]() 上的任意一点,点
上的任意一点,点![]() 是图形
是图形![]() 上的任意一点,若存在直线
上的任意一点,若存在直线![]() :
:![]() 满足
满足![]() 且
且![]() ,则称直线
,则称直线![]() :
:![]() 是图形
是图形![]() 与
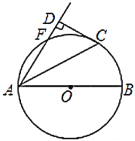
与![]() 的“隔离直线”,如图
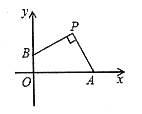
的“隔离直线”,如图![]() ,直线
,直线![]() :
:![]() 是函数
是函数![]() 的图像与正方形
的图像与正方形![]() 的一条“隔离直线”.
的一条“隔离直线”.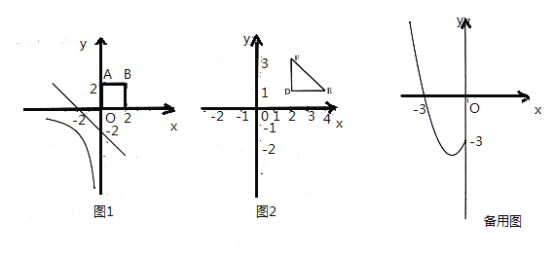
(1)在直线①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,是图
中,是图![]() 函数
函数![]() 的图像与正方形
的图像与正方形![]() 的“隔离直线”的为 .
的“隔离直线”的为 .
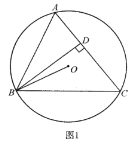
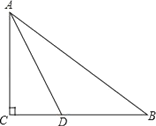
(2)如图![]() ,第一象限的等腰直角三角形
,第一象限的等腰直角三角形![]() 的两腰分别与坐标轴平行,直角顶点
的两腰分别与坐标轴平行,直角顶点![]() 的坐标是
的坐标是![]() ,⊙O的半径为
,⊙O的半径为![]() ,是否存在
,是否存在![]() 与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式:若不存在,请说明理由;
与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式:若不存在,请说明理由;
(3)正方形![]() 的一边在
的一边在![]() 轴上,其它三边都在
轴上,其它三边都在![]() 轴的左侧,点
轴的左侧,点![]() 是此正方形的中心,若存在直线
是此正方形的中心,若存在直线![]() 是函数
是函数![]() 的图像与正方形
的图像与正方形![]() 的“隔离直线”,请直接写出
的“隔离直线”,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①④;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据的“隔离直线”的定义即可解决问题;
(2)存在,连接![]() ,求得
,求得![]() 与
与![]() 垂直且过
垂直且过![]() 的直接就是“隔离直线”,据此即可求解;
的直接就是“隔离直线”,据此即可求解;
(3)分两种情形正方形在x轴上方以及在x轴下方时,分别求出正方形的一个顶点在直线![]() 上时的t的值即可解决问题.
上时的t的值即可解决问题.
(1)根据的“隔离直线”的定义可知![]() ,是图1函数
,是图1函数![]() 的图象与正方形OABC的“隔离直线”;直线
的图象与正方形OABC的“隔离直线”;直线![]() 也是图1函数
也是图1函数![]() 的图象与正方形OABC的“隔离直线”;而
的图象与正方形OABC的“隔离直线”;而![]() 与
与![]() 不满足图1函数
不满足图1函数![]() 的图象与正方形OABC的“隔离直线”的条件;
的图象与正方形OABC的“隔离直线”的条件;
故答案为:①④;
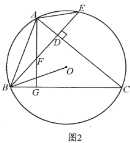
(2)存在,
理由如下:
连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,如图,
,如图,
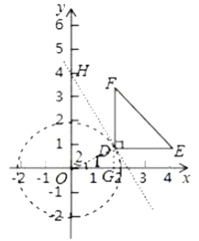
在Rt△DGO中,![]() ,
,
∵⊙O的半径为![]() ,
,
∴点D在⊙O上.
过点D作DH⊥OD交y轴于点H,
∴直线DH是⊙O的切线,也是△EDF与⊙O的“隔离直线”.
设直线OD的解析式为![]() ,
,
将点D(2,1)的坐标代入得![]() ,
,
解得:![]() ,
,
∵DH⊥OD,
∴设直线DH的解析式为![]() ,
,
将点D(2,1)的坐标代入得![]() ,
,
解得:![]() ,
,
∴直线DH的解析式为![]() ,
,
∴“隔离直线”的表达式为![]() ;
;
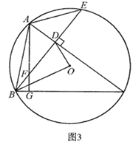
(3)如图:
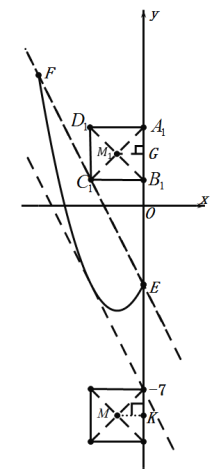
由题意点F的坐标为(![]() ),
),
当直线![]() 经过点F时,
经过点F时,![]() ,
,
∴![]() ,
,
∴直线![]() ,即图中直线EF,
,即图中直线EF,
∵正方形A1B1C1D1的中心M(1,t),
过点![]() 作
作![]() ⊥y轴于点G,
⊥y轴于点G,
∵点![]() 是正方形的中心,且
是正方形的中心,且![]() ,
,
∴B1C1![]() ,
,![]() ,
,
∴正方形A1B1C1D1的边长为2,
当![]() 时,
时,![]() ,
,
∴点C1的坐标是(![]() ),此时直线EF是函数
),此时直线EF是函数![]() )的图象与正方形A1B1C1D1的“隔离直线”,
)的图象与正方形A1B1C1D1的“隔离直线”,
∴点![]() 的坐标是(-1,2),
的坐标是(-1,2),
此时![]() ;
;
当直线![]() 与
与![]() 只有一个交点时,
只有一个交点时,
![]() ,消去y得到
,消去y得到![]() ,
,
由![]() ,可得
,可得![]() ,
,
解得:![]() ,
,
同理,此时点M的坐标为:(![]() ),
),
∴![]() ,
,
根据图象可知:
当![]() 或
或![]() 时,直线
时,直线![]() 是函数
是函数![]() )的图象与正方形A1B1C1D1的“隔离直线”.
)的图象与正方形A1B1C1D1的“隔离直线”.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案