题目内容
(1)解方程:(x-3)2-2x(x-3)=0
(2)用配方法确定二次函数y=-x2+5x+3的图像的开口方向、对称轴和顶点坐标.
(1)x1=3,x2=-3.(2)开口方向向下、对称轴为直线x= 、顶点坐标为(
、顶点坐标为( ,
, ).
).
【解析】
试题分析:(1)首先利用提公因式法,将(x-3)2-2x(x-3)因式分解,然后由x-3=0或x+3=0,即可求得答案.
(2)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
试题解析:(1)∵(x-3)2-2x(x-3)=0,
∴(x-3)(x+3)=0,
∴x-3=0或x+3=0,
∴x1=3,x2=-3.
∴原方程的解为:x1=3,x2=-3.
(2)y=-x2+5x+3=-(x2-5x)+3
=-(x2-5x+ -
- )+3
)+3
=-(x- )2+
)2+
所以:二次函数y=-x2+5x+3的图像的开口方向向下、对称轴为直线x= 、顶点坐标为(
、顶点坐标为( ,
, ).
).
考点:1.解一元二次方程-因式分解法.2.二次函数的三种形式;3.二次函数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则
,则 D、若
D、若 ,则
,则

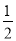 . 其中正确的说法是( )
. 其中正确的说法是( )
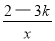 的图象的每一条曲线上,y都随x的增大而增大,写出一个符合题意的k的值 。
的图象的每一条曲线上,y都随x的增大而增大,写出一个符合题意的k的值 。

