题目内容
17.解不等式(组).(1)3(x+1)-6≤4x
(2)$\left\{\begin{array}{l}2x-1≥-1\\ 3x+1<4\end{array}\right.$,并把解集在数轴上表示出来.
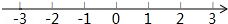
分析 (1)先去括号、移项、合并同类项、系数化为1即可求出x的取值范围.
(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:(1)去括号得,3x+3-6≤4x,
移项得,3x-4x≤6-3,
合并同类项得,-x≤3,
系数化为1得,x≥-3.
故此不等式的解集为:x≥-3.
(2)$\left\{\begin{array}{l}{2x-1≥-1①}\\{3x+1<4②}\end{array}\right.$,
由①得,x≥0,
由②得,x<1,
故此不等式组的解集为:0≤x<1.
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
5.点A(-3,5)先向右平移3个单位长度,再向上平移5个单位长度后与点B重合,则点B的坐标是( )
| A. | (0,0) | B. | (-6,0) | C. | (0,10) | D. | (-6,10) |
7.某鞋店销售同种品牌不同尺码的男鞋,采购员再次进货时,对于男鞋的尺码,他最关注的是( )
| A. | 方差 | B. | 众数 | C. | 中位数 | D. | 平均数 |
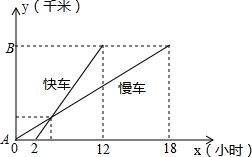 一慢车和一快车沿相同路线从A地到相距1200千米的B地,所行路程与时间的函数图象如图所示,试根据图象,回答下列问题:
一慢车和一快车沿相同路线从A地到相距1200千米的B地,所行路程与时间的函数图象如图所示,试根据图象,回答下列问题: 如图所示的图案绕其旋转中心旋转后能够与自身重合,那么它的旋转角的度数可能是72°(答案不唯一)(填写一个你认为正确的答案).
如图所示的图案绕其旋转中心旋转后能够与自身重合,那么它的旋转角的度数可能是72°(答案不唯一)(填写一个你认为正确的答案).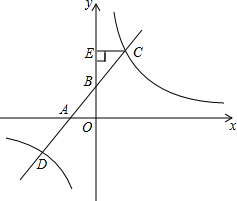 如图,直线y1=kx+2与x轴、y轴分别交于点A、B,点C(1,a)、D(b,-2)是直线与双曲线y2=$\frac{m}{x}$的两个交点,过点C作CE⊥y轴于点E,且△BCE的面积为1.
如图,直线y1=kx+2与x轴、y轴分别交于点A、B,点C(1,a)、D(b,-2)是直线与双曲线y2=$\frac{m}{x}$的两个交点,过点C作CE⊥y轴于点E,且△BCE的面积为1.