题目内容
某公司有A产品40件,B产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润 (元) 如下表所示:
A产品的利润/元 | B产品的利润/元 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1) 设分配给甲店A产品x件,这家公司卖出这100件产品的总利润为W (元),求W关于x的函数关系式,并求出x的取值范围;
(2) 若要求总利润不低于17560元;有多少种不同的分配方案? 并将各种方案设计出来;
(3) 为了促销,公司决定仅对甲店A产品让利销售,每件让利a元,但让利后A产品的每件利润仍高于甲店B产品的每件利润.甲店的B产品以及乙店的A,B产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
(1)10≤x≤40; (2)详见解析;(3)当x=10时,利润最大. 【解析】试题分析:(1)分配给甲店A型产品x件,则分配给甲店B型产品(70-x)件,分配给乙店A型产品(40-x)件,分配给乙店B型产品(x-10)件,根据总利润等于各利润之和进行求解;根据x≥0,40-x≥0,30-(40-x)≥0可以求出取值范围;(2)、根据W≤17560得到x的取值范围,和(1)中的取值范围得到x...甲乙两人在同一条道路上同时出发,同时行进,甲步行,乙骑车,出发时甲在前,乙在后,图中l甲,l乙,分别表示出发后甲、乙离出发地的路程s(km)和经历的时间t(h)的关系.
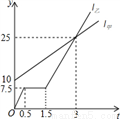
(1)乙出发时甲、乙相距___km.
(2)乙骑行一段路后,自行车发生故障,进行修理,所用的时间是___h.
(3)图象l甲,l乙相交的实际意义是什么?
(4)若乙的自行车没有故障,保持出发时的速度前进,求甲,乙相遇的时间和地点.
查看答案如图,直线y=﹣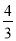 x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
(1)点B′的坐标;
(2)直线AM所对应的函数关系式.
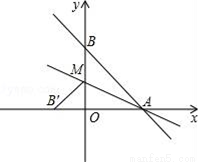
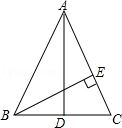
如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN⊥AB,PM⊥AC,垂足分别为点N,M.求证:BN=CM
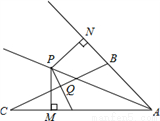
如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
求下列各式中的x.
(1)4x2 =81;
(2)(x+1)3-27=0.
(3)计算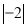 +(3-π)0-2-1+
+(3-π)0-2-1+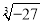
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-2,1).
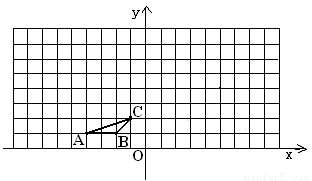
(1)画出△ABC绕C点顺时针旋转90°后得到的△A1B1C1并写出A1点的坐标;
(2)以原点O为位似中心,位似比为2,在第二象限内作△ABC的位似图形△A2B2C2,并写出C2的坐标.
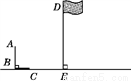
(1)图略 (-2,5) ;(2)图略(-2,4) 【解析】试题分析:(1)根据△ABC绕C点顺时针旋转90°的△A1B1C1,得出各对应点的坐标即可得出答案; (2)根据位似图形的性质得出对应点位置即可得出答案. 试题解析:(1)如图所示:A1(-2,5); (2)如图所示:C2(-2,4).如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
解方程:x+5=x2-25.
查看答案如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=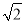 AE2;④S△ABC=4S△ADF.其中正确的有___________.
AE2;④S△ABC=4S△ADF.其中正确的有___________.
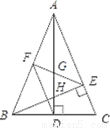
如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=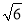 ,AD=2.当AB=_______时,△ABC与△ACD相似.
,AD=2.当AB=_______时,△ABC与△ACD相似.
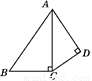
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 _______
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列各等式中,正确的是( )
A. 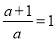 B.
B. 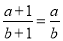
C. 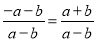 D.
D. 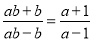
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
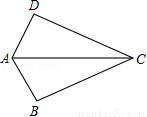
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案下列各式由左边到右边的变形中,是因式分解的是( )
A.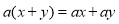
B.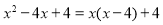
C.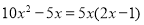
D.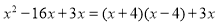
下列各式中,分式的个数为 ( )
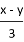 ,
,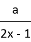 ,
,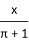 ,
,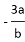 ,
,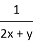 ,
,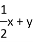 ,
,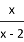 .
.
A. 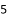 个 B.
个 B. 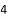 个 C.
个 C. 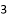 个 D.
个 D. 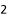 个
个
在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如下表:
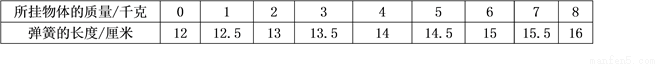
(1)上表中,自变量是 ,因变量是 ;
(2)弹簧不挂物体的长度是 ;
(3)如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势是 ,写出y与x的关系式 ;
(4)如果弹簧最大挂质量为25千克,你能计算出当挂重为14千克时,弹簧的长度是多少?
查看答案为了绿化环境,育英中学八年级三班同学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:
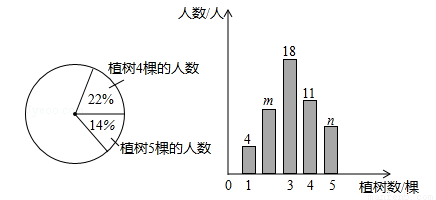
(1)八年级三班共有多少名同学?
(2)条形统计图中,m= ,n= .
(3)扇形统计图中,试计算植树2棵的人数所对应的扇形圆心角的度数.
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图所示,边长为a的正方形中阴影部分的面积为( )
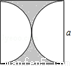
A. a2﹣π(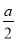 )2 B. a2﹣πa2 C. a2﹣πa D. a 2﹣2πa
)2 B. a2﹣πa2 C. a2﹣πa D. a 2﹣2πa
下列各组整式中不是同类项的是( )
A. 3a2b与﹣2ba2 B. 2xy与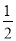 yx C. 16与﹣
yx C. 16与﹣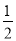 D. ﹣2xy2与3yx2
D. ﹣2xy2与3yx2
单项式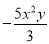 的系数与次数分别是( )
的系数与次数分别是( )
A. 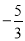 和3 B. ﹣5和3 C.
和3 B. ﹣5和3 C. 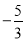 和2 D. ﹣5和2
和2 D. ﹣5和2
对于圆的周长公式C=2πR,下列说法错误的是( )
A. π是变量 B. R、C是变量 C. R是自变量 D. C是因变量
查看答案下列式子中,符合代数式的书写格式的是( )
A.(a﹣b)×7 B.3a÷5b C.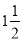 ab D.
ab D.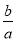
今年某县有1万名初中和小学生参加全国义务教育质量抽测,为了了解1万名学生的抽测成绩,从中抽取500名学生抽测成绩进行统计分析,在这个问题中数据500是( )
A. 总体 B. 个体 C. 一个样本 D. 样本容量
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
光年是天文学中的距离单位,1光年大约是9500 000 000 000 km,用科学记数法可表示为( )
A、950×1010 km B、95×1011 km C、9.5×1012 km D、0.95×1013 km
C 【解析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数 将9500000000000用科学记数法表示为:9.5×1012 故选C如图示,数轴上点A所表示的数的绝对值为( )
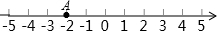
A.2 B.﹣2 C.±2 D.以上均不对
查看答案在数﹣(﹣3),0,(﹣3)2,|﹣9|,﹣14中,正数的有( )个.
A. 2 B. 3 C. 4 D. 5
查看答案﹣ 的相反数是( )
的相反数是( )
A. ﹣5 B. 5 C. ﹣ D.
D. 
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
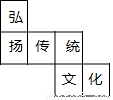
A. 传 B. 统 C. 文 D. 化
查看答案某公司有A产品40件,B产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润 (元) 如下表所示:
A产品的利润/元 | B产品的利润/元 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1) 设分配给甲店A产品x件,这家公司卖出这100件产品的总利润为W (元),求W关于x的函数关系式,并求出x的取值范围;
(2) 若要求总利润不低于17560元;有多少种不同的分配方案? 并将各种方案设计出来;
(3) 为了促销,公司决定仅对甲店A产品让利销售,每件让利a元,但让利后A产品的每件利润仍高于甲店B产品的每件利润.甲店的B产品以及乙店的A,B产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
求下列各式中的x.
(1)4x2 =81;
(2)(x+1)3-27=0.
(3)计算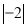 +(3-π)0-2-1+
+(3-π)0-2-1+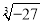
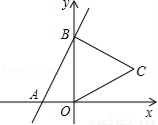
如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .
将一次函数y=-x+3的图像沿y轴向下平移2个单位长度,所得图像对应的函数表达式为__________.
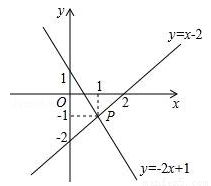
查看答案如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组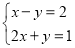 的解是 .
的解是 .
已知a、b、c是△ABC的三边长,且满足关系式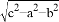 +|a﹣b|=0,则△ABC的形状为_____.
+|a﹣b|=0,则△ABC的形状为_____.
在平面直角坐标系中,点 (-3,4) 关于y轴对称的点的坐标是__________.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
先化简,再求值:x2﹣3(2x2﹣4y)+2(x2﹣y)其中x=﹣2,y=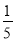 .
.
化简:
(1)﹣3xy﹣2y2+5xy﹣4y2
(2)2(5a2﹣2a)﹣4(﹣3a+2a2)
查看答案计算:
(1)3+(﹣11)﹣(﹣9)
(2)(﹣7)×5﹣(﹣36)÷4
(3)(1﹣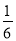 +
+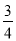 )×(﹣24)
)×(﹣24)
(4)﹣14+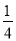 ×[2×(﹣6)﹣(﹣4)2].
×[2×(﹣6)﹣(﹣4)2].
让我们轻松一下,做一个数字游戏:
第一步:取一个自然数n1=5,计算n12+1得a1;
第二步:算出a1的各位数字之和得n2,计算n22+1得a2;
第三步:算出a2的各位数字之和得n3,再计算n32+1得a3;
…
依此类推,则a2013=_____.
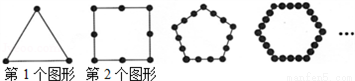
查看答案如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是___________.
定义新运算符号“⊕”如下:a⊕b=a﹣b﹣1,则2⊕(﹣3)=_____.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
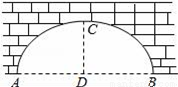
如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,求拱桥的半径.
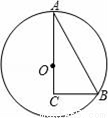
如图,Rt△ABC中,∠C=90°、∠A=30°,在AC边上取点O画圆,使⊙O经过A、B两点,下列结论正确的序号是____________
①AO=2CO;②AO=BC;③以O为圆心,以OC为半径的圆与AB相切;④延长BC交⊙O与D,则A、B、D是⊙O的三等分点.
在同一平面上一点P到⊙O的距离最长为7cm,最短为3m,则⊙O的半径为____cm.
查看答案己知拋物线y=x2﹣2x﹣3,当﹣2≤x≤0时,y的取值范围是____________
查看答案已知方程x2+mx﹣3=0的一个根是1,则它的另一个根是______.
查看答案如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:
①abc<0;
②2a﹣b=0;
③4a+2b+c<0;
④若(﹣5,y1),(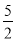 ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.
其中说法正确的是( )
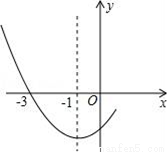
A. ①② B. ②③ C. ①②④ D. ②③④
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

