题目内容
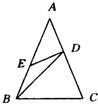 11、已知:如图所示,在△ABC中,AB=AC,D为AC上一点,且BD=BC,E为AB上一点,且AD=DE=EB,那么∠A的度数是
11、已知:如图所示,在△ABC中,AB=AC,D为AC上一点,且BD=BC,E为AB上一点,且AD=DE=EB,那么∠A的度数是45
度.分析:本题中相等的边较多,且都是在同一个三角形中,因为求“角”的度数,将“等边”转化为有关的“等角”,充分理论用“等边对等角”这一性质,再联系三角形内角和为180°求解此题.
解答:解:∵AD=DE,
∴∠A=∠AED,
∵DE=EB,
∴∠EBD=∠EDB,
∵∠AED=∠EBD+∠EDB=2∠EBD,
∴∠A=2∠EBD,
∵BD=BC,
∴∠C=∠BDC,
∵∠BDC=∠A+∠EBD=3∠EBD,
∴∠C=3∠EBD,
∵AB=AC,
∴∠C=∠ABC,
∵∠A+∠C+∠ABC=180°,
∴∠A+2∠C=180°,
2∠EBD+2×3∠EBD=8∠EBD=4∠A=180°.
∴∠A=45°.
∴∠A=∠AED,
∵DE=EB,
∴∠EBD=∠EDB,
∵∠AED=∠EBD+∠EDB=2∠EBD,
∴∠A=2∠EBD,
∵BD=BC,
∴∠C=∠BDC,
∵∠BDC=∠A+∠EBD=3∠EBD,
∴∠C=3∠EBD,
∵AB=AC,
∴∠C=∠ABC,
∵∠A+∠C+∠ABC=180°,
∴∠A+2∠C=180°,
2∠EBD+2×3∠EBD=8∠EBD=4∠A=180°.
∴∠A=45°.
点评:本题考查了等腰三角形的性质及三角形的内角和定理、三角形外角的性质;解题中反复运用了“等边对等角”,将已知的等边转化为有关角的关系,并联系三角形的内角和及三角形一个外角等于与它不相邻的两个内角的和的性质求解有关角的度数问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 阅读下述说明过程,讨论完成下列问题:
阅读下述说明过程,讨论完成下列问题: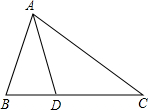 已知:如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
已知:如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.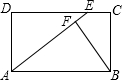 已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.
已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.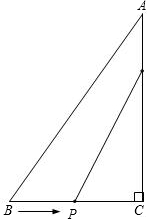 同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.
同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.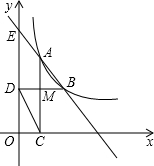 点M,连接DC.
点M,连接DC.