题目内容
方程|x2-4x-5|=m有两个不同的实数解，求m的取值范围．
考点：根的判别式
专题：分类讨论
分析：先将原绝对值方程转化为|（x-2）2-9|=m，据此作出该方程的图象；然后根据图象填空．
解答：
解：由原方程，得
|（x-2）2-9|=m，
该函数图象为：
根据图示知，实数m的取值范围是m=0或m＞9．
解：由原方程，得|（x-2）2-9|=m，
该函数图象为：
根据图示知，实数m的取值范围是m=0或m＞9．
点评：本题考查了含绝对值符号的一元二次方程．本题采用了“数形结合”的数学思想．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
下列式子中分解因式正确的是（ ）
| A、x2-4x+4=x（x-4）+4 |
| B、x2+2x+1=（x+1）2 |
| C、a2-b2=（a-b）2 |
| D、2x-4=2（x-4） |
如图，PA、PB切⊙O于点A、B，PA=6，∠APB=60°，求阴影部分周长和面积．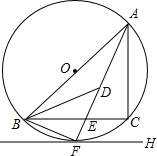
如图，⊙O是△ABC的外接圆，FH是⊙O的切线，切点为F，FH∥BC，连结AF交BC于E，∠ABC的平分线BD交AF于D，连结BF．
如图，△ABD、△BCE、△ACF均为等边三角形，请回答下列问题（不要求证明）