题目内容
20.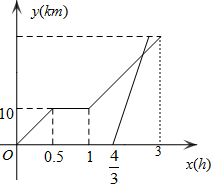 周末,天气晴朗,小明骑自行车从家里出发到野外郊游.小明从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,小明离家后3小时到达乙地.如图是他们离家的路程y(千米)与小明离家时间x(小时)的函数图象.已知妈妈驾车的速度是小明骑自行车速度的3倍.
周末,天气晴朗,小明骑自行车从家里出发到野外郊游.小明从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,小明离家后3小时到达乙地.如图是他们离家的路程y(千米)与小明离家时间x(小时)的函数图象.已知妈妈驾车的速度是小明骑自行车速度的3倍.(1)小明骑自行车的速度为20千米/小时;小明在甲地游玩的时间为0.5小时;
(2)乙地距离小明家有50千米;
(3)小明从家出发多少小时的时候被妈妈追上?此时离家多远?
分析 (1)根据速度=路程÷时间即可得出小明骑自行车的速度,再结合图形与x轴平行的线段即可得出小明在甲地游玩的时间;
(2)根据路程=速度×时间,代入小明骑自行车的速度以及骑行的时间即可得出结论;
(3)利用待定系数法求出小明在1≤x≤3时间段离家的路程y(千米)与离家时间x(小时)的函数关系式以及妈妈离家的路程y(千米)与小明离家时间x(小时)的函数关系式,再联立两函数关系式成方程组,解之即可得出结论.
解答 解:(1)小明骑自行车的速度为:10÷0.5=20(千米/小时);
小明在甲地游玩的时间为:1-0.5=0.5(小时).
故答案为:20;0.5.
(2)乙地到小明家的距离为:20×(3-0.5)=50(千米).
故答案为:50.
(3)设小明在1≤x≤3时间段离家的路程y(千米)与离家时间x(小时)的函数关系式为y=20x+a,妈妈离家的路程y(千米)与小明离家时间x(小时)的函数关系式为y=60x+b,
将(1,10)代入y=20x+a中,得:10=20+a,
解得:a=-10,
∴小明在1≤x≤3时间段离家的路程y(千米)与离家时间x(小时)的函数关系式为y=20x-10;
将($\frac{4}{3}$,0)代入y=60x+b中,得:0=60×$\frac{4}{3}$+b,
解得:b=-80,
∴妈妈离家的路程y(千米)与小明离家时间x(小时)的函数关系式为y=60x-80.
联立两函数关系式成方程组,得:
$\left\{\begin{array}{l}{y=20x-10}\\{y=60x-80}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{7}{4}}\\{y=25}\end{array}\right.$,
∴小明从家出发$\frac{7}{4}$小时的时候被妈妈追上,此时离家25千米.
点评 本题考查了一次函数的应用,观察函数图象找出点的坐标利用待定系数法求出函数解析式是解题的关键.

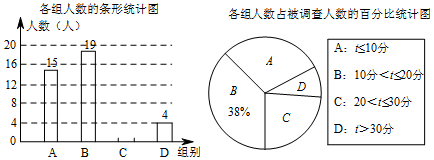
 按下列要求画图并填空:
按下列要求画图并填空: