题目内容
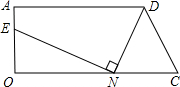 如图所示,梯形AOCD中,∠AOC=90°,AD=9,OC=10,AO=4在线段OC上任取一点N(不与O、C重合),连接DN,作NE⊥DN,与直线AO交于点E.
如图所示,梯形AOCD中,∠AOC=90°,AD=9,OC=10,AO=4在线段OC上任取一点N(不与O、C重合),连接DN,作NE⊥DN,与直线AO交于点E.(1)当CN=2时,求OE;
(2)若CN=t,OE=s,求s关于自变量t的函数关系式;
(3)探索与研究:如图2所示,分别以AO、OC所在的直线为y轴与x轴,O为原点,建立如图所示的直角坐标系,动点M从点O沿线段OC向C点运动,动点N从点C沿线段CO向点O同时等速运动,
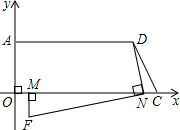 设现有一点F(x,y)满足MF⊥MN,NF⊥ND,试用含x的式子表示y.
设现有一点F(x,y)满足MF⊥MN,NF⊥ND,试用含x的式子表示y.
分析:由直角三角形的特性确定两个相等的角方便之间的关系转换,求s关于自变量t的函数关系式时要分清①0<t<1,②t>1两种情况.
解答: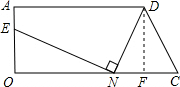 解:(1)如图所示,作DF⊥OC于F,
解:(1)如图所示,作DF⊥OC于F,
由题意知,CN=2,AD=9,OC=10.
∵AOCD是梯形且∠AOC=90°,
∴OF=AD=9,CF=OC-OF=1,NF=CN-CF=1,DF=OA=4.
∴在Rt△DFN中,tan∠DNF=
=
=4.
又∵NE⊥DN,∠AOC=90°,
∴∠DNF=∠OEN,tan∠OEN=tan∠DNF=4.
∴OE=
=
=2;
(2)如图所示: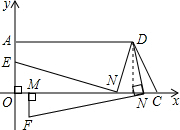
①当0<t<1时由(1)知CF=1,所以此时N点在F点右侧,E点在y轴负半轴
∵∠DNF=∠OEN,
∴tan∠DNF=
=
=tan∠OEN=
=
,
即
=
,
∴s=
.
②当t>1时,如图所示N点在F点左侧,E点则在y轴正半轴.
∵∠DNF=∠OEN,
∴tan∠DNF=
=tan∠OEN=
,
即
=
,
∴S=
;
(3)如图所示:由图知点F在第四象限,
∵MF⊥MN,NF⊥ND,点F(x,y),M点、N点同时等速运动,
∴CN=OM=x.
又∵∠MFN+∠MNF=∠MNF+∠DNM=90°,
∴∠MFN=∠DNM,
即:tan∠MFN=
=
=tan∠DNM=
=
,y<0,
∴y=-
x2+3x-
.
 解:(1)如图所示,作DF⊥OC于F,
解:(1)如图所示,作DF⊥OC于F,由题意知,CN=2,AD=9,OC=10.
∵AOCD是梯形且∠AOC=90°,
∴OF=AD=9,CF=OC-OF=1,NF=CN-CF=1,DF=OA=4.
∴在Rt△DFN中,tan∠DNF=
| DF |
| NF |
| 4 |
| 1 |
又∵NE⊥DN,∠AOC=90°,
∴∠DNF=∠OEN,tan∠OEN=tan∠DNF=4.
∴OE=
| ON |
| tan∠OEN |
| 8 |
| 4 |
(2)如图所示:

①当0<t<1时由(1)知CF=1,所以此时N点在F点右侧,E点在y轴负半轴
∵∠DNF=∠OEN,
∴tan∠DNF=
| DF |
| FN |
| 4 |
| 1-t |
| OF |
| OE |
| 10-t |
| s |
即
| 4 |
| 1-t |
| 10-t |
| s |
∴s=
| t2-11t+10 |
| 4 |
②当t>1时,如图所示N点在F点左侧,E点则在y轴正半轴.
∵∠DNF=∠OEN,
∴tan∠DNF=
| DN |
| FN |
| OF |
| OE |
即
| 10-t |
| s |
| 4 |
| t-1 |

∴S=
| -t2+11t-10 |
| 4 |
(3)如图所示:由图知点F在第四象限,
∵MF⊥MN,NF⊥ND,点F(x,y),M点、N点同时等速运动,
∴CN=OM=x.
又∵∠MFN+∠MNF=∠MNF+∠DNM=90°,
∴∠MFN=∠DNM,
即:tan∠MFN=
| MN |
| MF |
| 10-2x |
| |y| |
| OA |
| 1-x |
| 4 |
| 1-x |
∴y=-
| 1 |
| 2 |
| 5 |
| 2 |
点评:此题考查学生结合变化的图象求函数关系式的能力,主要运用直角三角形的特殊性质和正切性质求解.

练习册系列答案
相关题目
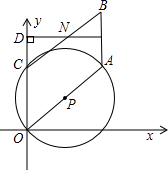 A、B两点不重合),点N是DM与BC的交点,设OD=t;
A、B两点不重合),点N是DM与BC的交点,设OD=t; 直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动(运动到点C为止).
直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动(运动到点C为止). 如图所示,梯形AOCD中,∠AOC=90°,AD=9,OC=10,AO=4在线段OC上任取一点N(不与O、C重合),连接DN,作NE⊥DN,与直线AO交于点E.
如图所示,梯形AOCD中,∠AOC=90°,AD=9,OC=10,AO=4在线段OC上任取一点N(不与O、C重合),连接DN,作NE⊥DN,与直线AO交于点E.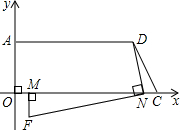 设现有一点F(x,y)满足MF⊥MN,NF⊥ND,试用含x的式子表示y.
设现有一点F(x,y)满足MF⊥MN,NF⊥ND,试用含x的式子表示y.