题目内容
利用二次函数的图象求一元二次方程x2-3x-6=0的近似根．
考点：图象法求一元二次方程的近似根
专题：数形结合
分析：根据函数与方程的关系，可得函数图象与x轴的交点的横坐标就是相应的方程的解．
解答：
解：方程x2-3x-6=0根是函数y=x2-3x-6与x轴交点的横坐标．
作出二次函数y=x2-3x-6的图象，如图所示，
由图象可知方程有两个根，一个在-2和-1之间，另一个在4和5之间．
先求-2和-1之间的根，
当x=-1.4时，y=0.16；当x=-1.3时，y=-0.41；
因此，x=-1.4是方程的一个近似根，
同理，x=4.4是方程的另一个近似根．
故一元二次方程x2-3x-6=0的近似根为x=-1.4或4.4．
解：方程x2-3x-6=0根是函数y=x2-3x-6与x轴交点的横坐标．作出二次函数y=x2-3x-6的图象，如图所示，
由图象可知方程有两个根，一个在-2和-1之间，另一个在4和5之间．
先求-2和-1之间的根，
当x=-1.4时，y=0.16；当x=-1.3时，y=-0.41；
因此，x=-1.4是方程的一个近似根，
同理，x=4.4是方程的另一个近似根．
故一元二次方程x2-3x-6=0的近似根为x=-1.4或4.4．
点评：本题考查了图象法求一元二次方程的近似根，二次函数图象与x轴交点的横坐标是相应的一元二次方程的解．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
如图，下列说法正确的是（ ）
| A、形状相同的两个三角形全等 |
| B、能完全重合的两个三角形全等 |
| C、两个等腰直角三角形全等 |
| D、面积相等的两个三角形全等 |
已知AC⊥AB，BD⊥AB，AD与BC相交于点E，EF⊥AB，设AC=p，BD=q，EF=r，求证：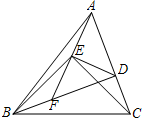
如图，在△ABC中，BD⊥AC，BD=AC，以BC为底边作等腰直角△BEC，连接AE并延长交BD于F点，下列结论：①△AEC≌△DEB；②AE⊥DE；③DE=DC；④S△AEB=S△CDE．其中正确的有（ ）个．