题目内容
 24、如图,△ABC的顶点A、B、C都在小正方形的顶点上,像这样的三角形叫做格点三角形.试在下面5×5的方格纸上按下列要求画格点三角形:
24、如图,△ABC的顶点A、B、C都在小正方形的顶点上,像这样的三角形叫做格点三角形.试在下面5×5的方格纸上按下列要求画格点三角形:(1)所画的三角形与△ABC全等且有1个公共顶点;
(2)所画的三角形与△ABC全等且有1条公共边;
(3)探索并计算一下与△ABC全等的格点三角形的个数有多少?并简要说明理由.
分析:根据题意,结合作图工具易画出图形.
(1)所画的三角形与△ABC全等且有1个公共顶点,也就是说画出的三角形可以分别与A、B或C三点为顶点做一个与△ABC全等的三角形即可;
(2)所画的三角形与△ABC全等且有1个公共边,也就是说所作出的与△ABC全等的三角形只要与AC、AB或BC重合便可;
(3)可以从C点坐标的变化得出符合要求的三角形,分四个方向分析得出答案.
(1)所画的三角形与△ABC全等且有1个公共顶点,也就是说画出的三角形可以分别与A、B或C三点为顶点做一个与△ABC全等的三角形即可;
(2)所画的三角形与△ABC全等且有1个公共边,也就是说所作出的与△ABC全等的三角形只要与AC、AB或BC重合便可;
(3)可以从C点坐标的变化得出符合要求的三角形,分四个方向分析得出答案.
解答:
 解:(1)如图①:
解:(1)如图①:
(2)如图②:
(3)格点三角形中此时同一个方向c点可以出现在15个位置,因为有4个方向,减掉它本身:
∴与△ABC全等的格点三角形的个数有:15×4-1=59个.

 解:(1)如图①:
解:(1)如图①:(2)如图②:
(3)格点三角形中此时同一个方向c点可以出现在15个位置,因为有4个方向,减掉它本身:
∴与△ABC全等的格点三角形的个数有:15×4-1=59个.
点评:此题主要考查了格点三角形的定义以及全等三角形的性质,要找出与△ABC全等的格点三角形的个数从顶点C分析得出符合要求的点是解决问题的关键.

练习册系列答案
相关题目
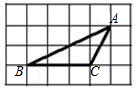 如图,△ABC的顶点都是正方形网格中的格点,则sin∠ABC等于
如图,△ABC的顶点都是正方形网格中的格点,则sin∠ABC等于



 如图,△ABC的顶点坐标分别为A ( 3,6 ),B ( 1,3 ),C ( 4,2 ).如果将△ABC绕C点顺时针旋转90°,得到△A′B′C′,那么点A的对应点A′的坐标为
如图,△ABC的顶点坐标分别为A ( 3,6 ),B ( 1,3 ),C ( 4,2 ).如果将△ABC绕C点顺时针旋转90°,得到△A′B′C′,那么点A的对应点A′的坐标为 如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1). 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移2格,再向上平移2格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移2格,再向上平移2格,其中每个格子的边长为1个单位长度.