题目内容
函数y= (k>0)的图象上两点A(x1,y1)和B(x2,y2),且x1>x2>0,分别过A,B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则S△AA1O________S△BB1O,若S△AA1O=2,则函数解析式为________.
(k>0)的图象上两点A(x1,y1)和B(x2,y2),且x1>x2>0,分别过A,B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则S△AA1O________S△BB1O,若S△AA1O=2,则函数解析式为________.
= y=
分析:利用反比例函数中,直角三角形的面积与反比例函数的系数大小之间的关系计算.
解答:两点A(x1,y1)和B(x2,y2),
在函数y= (k>0)的图象上,
(k>0)的图象上,
因而代入得到:k=x1y1=x2y2,
则S△AA1O= x1y1,S△BB1O=
x1y1,S△BB1O= x2y2,
x2y2,
则S△AA1O=S△BB1O;
设A点的坐标是(m,n),
则S△AA1O= mn=2,
mn=2,
则mn=4,
设函数的解析式是y= ,
,
A点的坐标是(m,n)一定满足函数解析式,
得到p=mn=4,
则函数解析式为y= .
.
则S△AA1O=S△BB1O(填“>”“=”或“<”),
若S△AA1O=2,则函数解析式为y= .
.
故答案为:=;y= .
.
点评:注意本题中的结论,反比例函数中,直角三角形的面积与反比例函数的系数大小之间的关系,需要熟记.

分析:利用反比例函数中,直角三角形的面积与反比例函数的系数大小之间的关系计算.
解答:两点A(x1,y1)和B(x2,y2),
在函数y=
 (k>0)的图象上,
(k>0)的图象上,因而代入得到:k=x1y1=x2y2,
则S△AA1O=
 x1y1,S△BB1O=
x1y1,S△BB1O= x2y2,
x2y2,则S△AA1O=S△BB1O;
设A点的坐标是(m,n),
则S△AA1O=
 mn=2,
mn=2,则mn=4,
设函数的解析式是y=
 ,
,A点的坐标是(m,n)一定满足函数解析式,
得到p=mn=4,
则函数解析式为y=
 .
.则S△AA1O=S△BB1O(填“>”“=”或“<”),
若S△AA1O=2,则函数解析式为y=
 .
.故答案为:=;y=
 .
.点评:注意本题中的结论,反比例函数中,直角三角形的面积与反比例函数的系数大小之间的关系,需要熟记.

练习册系列答案
相关题目
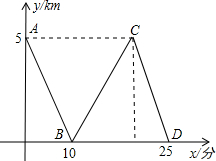 小明家、小亮家、学校在一条直的街道上,平时他俩乘同一校车上学,小明家距学校比小亮家远,每天小明比小亮早5分钟乘上校车上学.某日,因小明比每天晚了5分钟赶不上校车,由爸爸开自家车送小明上学.设两车均匀速行驶,小亮乘车时间为x(分),小明与小亮之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
小明家、小亮家、学校在一条直的街道上,平时他俩乘同一校车上学,小明家距学校比小亮家远,每天小明比小亮早5分钟乘上校车上学.某日,因小明比每天晚了5分钟赶不上校车,由爸爸开自家车送小明上学.设两车均匀速行驶,小亮乘车时间为x(分),小明与小亮之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象解决以下问题: (2013•大庆)如图,已知一次函数y=k1x+b(k1≠0)的图象分别与x轴,y轴交于A,B两点,且与反比例函数y=
(2013•大庆)如图,已知一次函数y=k1x+b(k1≠0)的图象分别与x轴,y轴交于A,B两点,且与反比例函数y=