题目内容
12.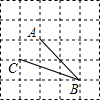 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )| A. | 2 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2\sqrt{5}}{5}$ |
分析 连接AC,根据勾股定理求出AC、BC、AB的长,根据勾股定理的逆定理得到△ABC是直角三角形,根据正切的定义计算即可.
解答 解:连接AC,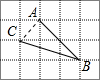
由网格特点和勾股定理可知,
AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,AB=2$\sqrt{2}$,BC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
AC2+AB2=10,BC2=10,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,
∴tan∠ABC=$\frac{AC}{AB}$=$\frac{\sqrt{2}}{2\sqrt{2}}$=$\frac{1}{2}$,
故选:C.
点评 本题考查的是锐角三角函数的定义、勾股定理及其逆定理的应用,熟记锐角三角函数的定义、掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
7.已知关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=4,求该矩形的面积.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=4,求该矩形的面积.
17.若单项式2x2ya+b与3xa-by4是同类项,则a,b的值分别是( )
| A. | a=3,b=1 | B. | a=-3,b=1 | C. | a=3,b=-1 | D. | a=-3,b=-1 |
1.在“书香伍家”读书节活动中,21名志愿者参与整理一批图书,每人每小时能登记录入20本或摆放120本书籍,为使每小时登记录入的书籍正好被及时摆放,设x名志愿者参与登记录入,其余志愿者参与摆放,则所列方程正确的是( )
| A. | 20x=120(21+x) | B. | 120x=20(21-x) | C. | 20x=120(21-x) | D. | 120x=20(21+x) |
2.某餐厅共有10名员工,所有员工的工资情况如下表:
则该餐厅所有员工工资的众数、中位数分别是( )
| 人员 | 经理 | 厨师 | 会计 | 保安 | 服务员 |
| 人数(人) | 1 | 2 | 1 | 1 | 5 |
| 工资(元) | 5000 | 4000 | 3500 | 3000 | 2000 |
| A. | 5000,3500 | B. | 5000,2500 | C. | 2000,3500 | D. | 2000,2500 |
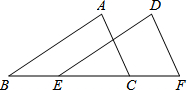 如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,那么还有对应角是∠B=∠E,∠C=∠F,对应边是BC=EF,AC=DF.
如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,那么还有对应角是∠B=∠E,∠C=∠F,对应边是BC=EF,AC=DF.