题目内容
在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm．（1）若花园的面积为192m2，求x的值；
（2）若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值．
考点：二次函数的应用,一元二次方程的应用
专题：几何图形问题
分析：（1）根据题意得出长×宽=192，进而得出答案；
（2）由题意可得出：S=x（28-x）=-x2+28x=-（x-14）2+196，再利用二次函数增减性求得最值．
（2）由题意可得出：S=x（28-x）=-x2+28x=-（x-14）2+196，再利用二次函数增减性求得最值．
解答：解：（1）∵AB=xm，则BC=（28-x）m，
∴x（28-x）=192，
解得：x1=12，x2=16，
答：x的值为12m或16m；
（2）∵AB=xm，
∴BC=28-x，
∴S=x（28-x）=-x2+28x=-（x-14）2+196，
∵在P处有一棵树与墙CD，AD的距离分别是15m和6m，
∵28-15=13，
∴6≤x≤13，
∴当x=13时，S取到最大值为：S=-（13-14）2+196=195，
答：花园面积S的最大值为195平方米．
∴x（28-x）=192，
解得：x1=12，x2=16，
答：x的值为12m或16m；
（2）∵AB=xm，
∴BC=28-x，
∴S=x（28-x）=-x2+28x=-（x-14）2+196，
∵在P处有一棵树与墙CD，AD的距离分别是15m和6m，
∵28-15=13，
∴6≤x≤13，
∴当x=13时，S取到最大值为：S=-（13-14）2+196=195，
答：花园面积S的最大值为195平方米．
点评：此题主要考查了二次函数的应用以及二次函数最值求法，得出S与x的函数关系式是解题关键．
练习册系列答案
相关题目
下列命题：
①对顶角相等；
②等腰三角形的两个底角相等；
③两直线平行，同位角相等．
其中逆命题为真命题的有（ ）
①对顶角相等；
②等腰三角形的两个底角相等；
③两直线平行，同位角相等．
其中逆命题为真命题的有（ ）
| A、①② | B、②③ | C、①③ | D、①②③ |
人们用“捡了芝麻，丢了西瓜”比喻因小失大，有人做过实验，2万粒芝麻的质量约80克，如果一个西瓜的质量为4千克，一粒芝麻的质量是这个西瓜质量的（ ）
| A、10-4倍 |
| B、10-5倍 |
| C、10-6倍 |
| D、10-7倍 |
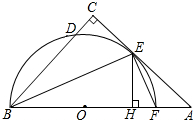如图，在△ABC中，∠C=90°，∠ABC的平分线交AC于点E，过点E作BE的垂线交AB于点F，⊙O是△BEF的外接圆．
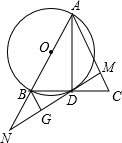如图，已知在△ABC中，AD是BC边上的中线，以AB为直径的⊙O交BC于点D，过D作MN⊥AC于点M，交AB的延长线于点N，过点B作BG⊥MN于G．
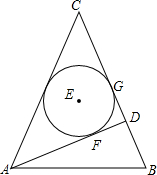如图，在等腰△ABC中，CA=CB，AD是腰BC边上的高，△ACD的内切圆⊙E分别与边AD、BC相切于点F、G，连AE、BE．
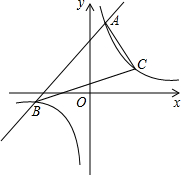已知一次函数y1=x+m的图象与反比例函数