题目内容
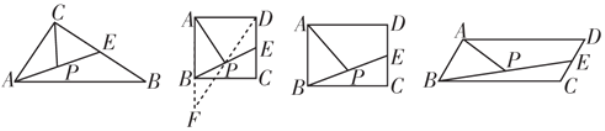
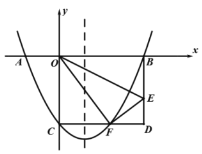
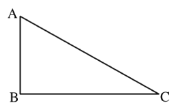
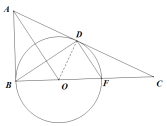
【题目】如图,在![]() 中,
中,![]() ,作
,作![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作圆.
为半径作圆.
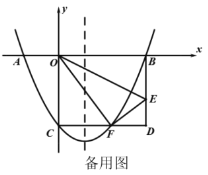
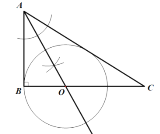
(1)依据题意补充完整图形;(尺规作图,保留作图痕迹,不写作法)
(2)求证:![]() 与直线
与直线![]() 相切;
相切;
(3)在(2)的条件下,若![]() 与直线
与直线![]() 相切的切点为
相切的切点为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ;其中
;其中![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据尺规作图的规则作图即可.
(2)根据角平分线证明边和角,再根据切线长定理求证即可.
(3)先在(2)的前提下,根据三角形相似,求出圆的半径,再根据△ODC∽△ABC求出AB即可.
(1)作图如下:
(2)证明:过点O作OD⊥AC,垂足为D.
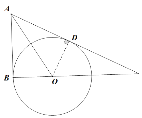
∵∠ABC=90°,
∴OB⊥AB,
∵AO平分∠BAC且OB⊥AB,OD⊥AC,
∴OB=OD,
∴⊙O与直线AC相切.
(2)由(1)可知,∠ODC=90°,
∵BF为直径
∴∠BDF=90°,
∴∠ODC=∠BDF,
∴∠BDO=∠CDF,
∵OB=OD,
∴∠BDO=∠DBO,
∴CDF=∠DBO,且∠DCF=∠BCD,
∴△DCF∽△BCD,
∴![]() ,
,
∵![]() ,CF=2,
,CF=2,
∴BC=6,
∴OB=OF=2,
∴OC=4,OD=2,
∵△ODC∽△ABC,
∴![]() ,OD=2,
,OD=2,![]()
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目