题目内容
10. 如图,在正方形ABCD的内部作等边△ADE,连接BE,CE,则∠BEC的度数为150°.
如图,在正方形ABCD的内部作等边△ADE,连接BE,CE,则∠BEC的度数为150°.
分析 根据等边三角形的性质可得AD=DE,根据正方形的性质可得AD=DC,从而得到DE=DC,再根据等边对等角可得∠CED=∠ECD,然后求出∠CDE=30°,再求出∠CED,再根据对称性利用周角等于360°列式计算即可得解.
解答 解:∵△ADE是等边三角形,
∴AD=DE,
∵四边形ABCD是正方形,
∴AD=DC,
∴DE=DC,
∴∠CED=∠ECD,
∴∠CDE=∠ADC-∠ADE=90°-60°=30°,
∴∠CED=∠ECD=$\frac{1}{2}$(180°-30°)=75°,
∴∠BEC=360°-75°×2-60°=150°.
故答案为:150°.
点评 本题考查了正方形的性质,等边三角形的性质,等腰三角形的判定与性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
1.在?ABCD中,AB=2,AC=$\sqrt{3}$,则平行四边形的最大面积为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
18. 如图,在四边形ABCD中,下列条件中可以判定AD∥BC的是( )
如图,在四边形ABCD中,下列条件中可以判定AD∥BC的是( )
 如图,在四边形ABCD中,下列条件中可以判定AD∥BC的是( )
如图,在四边形ABCD中,下列条件中可以判定AD∥BC的是( )| A. | ∠1=∠3 | B. | ∠2=∠4 | C. | ∠B=∠D | D. | ∠B+∠BCD=180° |
15.一个长方形在平面直角坐标系中,它的三个顶点的坐标分别为(-3,-1),(2,-1),(2,2),则第四个顶点的坐标为( )
| A. | (-3,2) | B. | (3,2) | C. | (-3,-4) | D. | (7,2) |
2.下列各组数不可能组成三角形的是( )
| A. | 3,4,5 | B. | 5,6,9 | C. | 5,7,12 | D. | 5,8,10 |
20.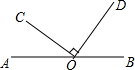 如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
 如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )| A. | 34° | B. | 44° | C. | 54° | D. | 64° |