题目内容
8.关于x的方程a(x+m)2+b=0的解是x1=3,x2=6(a,m,b均为常数,a≠0),则关于a(x+m+2)2+b=0的解是x1=1,x2=4.分析 把后面一个方程中的x+2看作整体,相当于前面一个方程中的x求解.
解答 解:∵关于x的方程a(x+m)2+b=0的解是x1=3,x2=6(a,m,b均为常数,a≠0),
∴方程a(x+m+2)2+b=0变形为a[(x+2)+m]2+b=0,即此方程中x+2=3或x+2=6,
解得x=1或x=4.
故方程a(x+m+2)2+b=0的解为x1=1,x2=4.
故答案为:x1=1,x2=4.
点评 此题主要考查了方程解的定义以及直接开方法求解.注意由两个方程的特点,运用整体思想进行简便计算.

练习册系列答案
相关题目
19.对角线互相平分的四边形一定是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
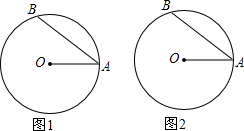 如图,⊙O的半径OA=5cm,AB是弦,∠OAB=30°,现有一动点C从A出发,沿弦AB运动到B,再从B沿劣弧BA回到点A.
如图,⊙O的半径OA=5cm,AB是弦,∠OAB=30°,现有一动点C从A出发,沿弦AB运动到B,再从B沿劣弧BA回到点A.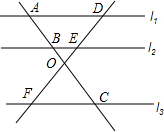 已知:l1∥l2∥l3,
已知:l1∥l2∥l3,