题目内容
建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为60°观察底部B的仰角为45°,求旗杆的角度(精确到0.1m).
分析:如图,由∠ADC=60°可以求出∠A=30°,就有AD=2CD=80m,由勾股定理就可以求出AC的值,在△BDC中由∠BDC=45°就可以求出BC的值,从而求出结论.
解答: 解:∵∠ACB=90°,∠ADC=60°,
解:∵∠ACB=90°,∠ADC=60°,
∴∠A=30°,
∴AD=2CD.
∵CD=40m,
∴AD=80m,
在Rt△ADC中,由勾股定理,得
AC=40
.
∵∠BDC=45°,
∴∠DBC=45°,
∴∠DBC=∠BDC,
∴BC=CD=40m,
∴AB=40
-40≈29.3m.
∴旗杆的高度为29.3m.
 解:∵∠ACB=90°,∠ADC=60°,
解:∵∠ACB=90°,∠ADC=60°,∴∠A=30°,
∴AD=2CD.
∵CD=40m,
∴AD=80m,
在Rt△ADC中,由勾股定理,得
AC=40
| 3 |
∵∠BDC=45°,
∴∠DBC=45°,
∴∠DBC=∠BDC,
∴BC=CD=40m,
∴AB=40
| 3 |
∴旗杆的高度为29.3m.
点评:本题考查了解直角三角形的运用,仰角的运用,直角三角形的性质的运用,勾股定理的运用,近似数的运用,解答时根据勾股定理求解是关键.

练习册系列答案
相关题目
 15、某建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为50°,观察底部B的仰角为45°,则旗杆的高度AB=
15、某建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为50°,观察底部B的仰角为45°,则旗杆的高度AB= 18、如图,建筑物BC上有一旗杆AB,在距BC20m的D处观察旗杆顶部A的仰角为50°,观察旗杆底部B的仰角为45°,求旗杆的高度.(精确到0.1m)(可供选用数据:sin50°=0.766,cos50°=0.642,tan50°=1.192)
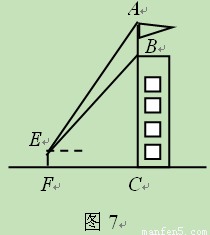
18、如图,建筑物BC上有一旗杆AB,在距BC20m的D处观察旗杆顶部A的仰角为50°,观察旗杆底部B的仰角为45°,求旗杆的高度.(精确到0.1m)(可供选用数据:sin50°=0.766,cos50°=0.642,tan50°=1.192)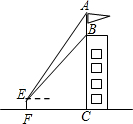 为52°、底部B的仰角为45°,小明的观测点与地面的距离EF为1.6m.
为52°、底部B的仰角为45°,小明的观测点与地面的距离EF为1.6m.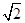 ≈1.41,sin52°≈0.79,tan52°≈1.28)
≈1.41,sin52°≈0.79,tan52°≈1.28)