Question

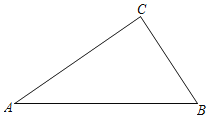
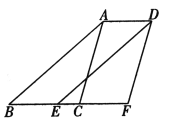
【题目】如图，△ABC是边长为2的等边三角形，将△ABC沿射线BC向右平移到△DCE，连接AD，BD，下列结论错误的是(　　)

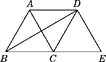
A.AD=BCB.BD⊥DE

C.四边形ACED是菱形D.四边形ABCD的面积为4

Answer 1

【答案】D

【解析】

由△ABC沿射线BC向右平移到△DCE，根据平移的性质：对应点的连线平行且相等得到AD与BC平行且相等，选项A正确，利用一组对边平行且相等的四边形为平行四边形得到ABCD为平行四边形，由三角形ABC为等边三角形可得出AB=BC，根据邻边相等的平行四边形为菱形可得出四边形ABCD为菱形，根据菱形的对角线互相垂直得到AC与BD垂直，再由平移的性质得到对应边平行，得到AC与DE平行，利用与平行线中的一条垂直，与另一条也垂直得到BD垂直于DE，选项B正确；同理可得出ACED为菱形，选项C正确；过A作AF垂直于BC，由三角形ABC为边长为2的等边三角形，根据三线合一得到BF为BC的一半，求出BF的长，在直角三角形ABF中，由AB及BF的长，利用勾股定理求出AF的长，然后利用底BC乘以高AF即可求出菱形ABCD的面积为2，选项D错误，即可得出满足题意的选项．

∵△ABC沿射线BC向右平移到△DCE，
∴AD=BC，AD∥BC，故选项A正确；
∴四边形ABCD为平行四边形，
又△ABC为等边三角形，∴AB=BC，
∴四边形ABCD为菱形，
∴AC⊥BD，
由平移可知：AC∥DE，
则DE⊥BD，故选项B正确；
∵△ABC沿射线BC向右平移到△DCE，
∴AD=CE，AD∥CE，
∴四边形ACED为平行四边形，
由平移可得△DCE也为等边三角形，
∴DE=CE，
∴四边形ACED为菱形，选项C正确；
过A作AF⊥BC，如图所示：

∵△ABC为边长为2的等边三角形，
∴BF=CF=BC=1，
在Rt△ABF中，AB=2，BF=1，
根据勾股定理得：AF=，
则S菱形ABCD=BCAF=2，选项D错误，
则原题结论错误的选项为D．
故选：D．