Question

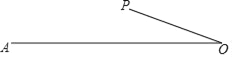
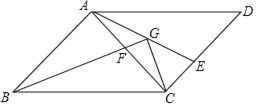
【题目】如图，已知在中，，将绕点逆时针旋转得到，交直线于．发现： ．

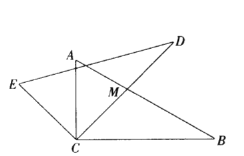
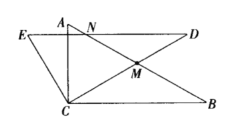
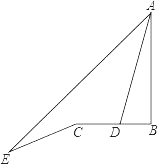
探究①：若恰好是的中点，交于，如图2，求的长；

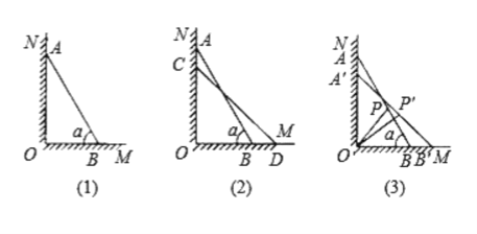
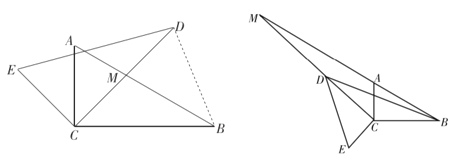
探究②：在旋转过程中，当是等腰三角形时，求点所旋转的路径长(保留)

Answer 1

【答案】发现：1；探究①：；探究②：或或或．

【解析】

发现：根据直角三角形中30度所对的直角边等于斜边的一半可得答案；

探究①：根据直角三角形斜边上中线的性质可得，，结合可得，然后根据进行计算；

探究②：分时和时两种情况，在每种情况下再分时和时两种情况，分别根据旋转的性质和等腰三角形的性质求出旋转角α，再根据弧长公式计算即可．

解：发现：由题意得；

探究①：∵，M是斜边的中点，，，

∴，，

∴，

∵将绕点逆时针旋转得到，

∴，

∵，

∴，

∴；

探究②：若时，连接，由题意得，

∵，

∴，

∵，

∴当时，有，即，

解得：，

∴点所旋转的路径长为：；

当时，有，即，

解得：，

∴点所旋转的路径长为：；

若时，

∵，

∵当时，有，

∴，

∵，

∴，

∴，

∴点所旋转的路径长为：，

同理，当时，有，

∴点所旋转的路径长为：，

综上所述，点所旋转的路径长为：或或或．