题目内容
17.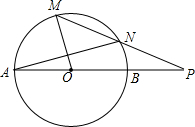 如图,AB为⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点M在⊙O上,PM交⊙O于另一点N,如果MO⊥AN,则tan∠OMN=$\frac{\sqrt{15}}{3}$.
如图,AB为⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点M在⊙O上,PM交⊙O于另一点N,如果MO⊥AN,则tan∠OMN=$\frac{\sqrt{15}}{3}$.
分析 连接BN,由AB为⊙O的直径,得到∠ANB=90°,由于MO⊥AN,推出BN∥OM,根据三角形的中位线定理得到BN=$\frac{1}{2}$OM=1,OC=$\frac{1}{2}$BN=$\frac{1}{2}$,在Rt△ABN中,根据勾股定理求出AN=$\sqrt{A{B}^{2}-B{N}^{2}}$=$\sqrt{15}$,得到CN=$\frac{\sqrt{15}}{2}$,即可得到结论.
解答  解:连接BN,
解:连接BN,
∵AB为⊙O的直径,
∴∠ANB=90°,
∵MO⊥AN,
∴BN∥OM,
∵BP=OB=2,
∴BN=$\frac{1}{2}$OM=1,
∵AO=BO,
∴OC=$\frac{1}{2}$BN=$\frac{1}{2}$,
∴CM=2-$\frac{1}{2}$=$\frac{3}{2}$,
在Rt△ABN中,AN=$\sqrt{A{B}^{2}-B{N}^{2}}$=$\sqrt{15}$,
∴CN=$\frac{\sqrt{15}}{2}$,
∴tan∠OMN=$\frac{CN}{CM}$=$\frac{\frac{\sqrt{15}}{2}}{\frac{3}{2}}$=$\frac{\sqrt{15}}{3}$.
故答案为:$\frac{\sqrt{15}}{3}$.
点评 本题考查了垂径定理,圆周角定理,勾股定理,三角形的中位线定理,熟练掌握各定理是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
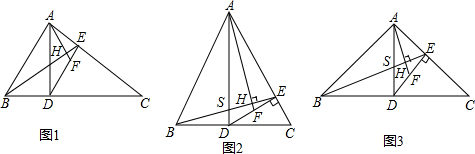
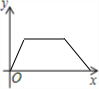
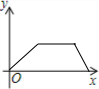
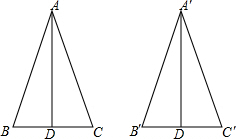 如图,AD、A′D′分别是BC和B′C′上的高,且∠B=∠B′,$\frac{A′D′}{AD}$=$\frac{B′C′}{BC}$,求证:△ABC∽△A′B′C.
如图,AD、A′D′分别是BC和B′C′上的高,且∠B=∠B′,$\frac{A′D′}{AD}$=$\frac{B′C′}{BC}$,求证:△ABC∽△A′B′C.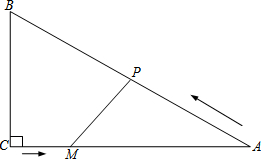 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M从点C出发,以每秒1cm的速度沿CA向终点A移动,同时动点P从点A出发,以每秒2cm的速度沿AB向终点B移动,连接PM,设移动时间为t(s)(0<t<2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M从点C出发,以每秒1cm的速度沿CA向终点A移动,同时动点P从点A出发,以每秒2cm的速度沿AB向终点B移动,连接PM,设移动时间为t(s)(0<t<2.5).