题目内容
15.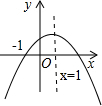 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的有( )个
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的有( )个①2a+b=0 ②当x<1时,y随x的增大而增大
③c<0 ④9a+3b+c=0 ⑤b2-4ac>0.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据对称轴x=-$\frac{b}{2a}$=1对①进行判断;根据二次函数的增减性可对②进行判断;由抛物线与y轴的交点在x轴上方得c>0,可对③进行判断;根据二次函数的对称性求出抛物线与x轴的另一个交点是(3,0),进而可对④进行判断;由抛物线与x轴交点的个数可对⑤进行判断.
解答 解:∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=1,∴2a+b=0,所以①正确;
∵抛物线开口向下,对称轴为直线x=1,∴当x<1时,y随x的增大而增大,所以②正确;
∵抛物线与y轴的交点在x轴上方,∴c>0,所以③错误;
∵抛物线与x轴的一个交点是(-1,0),对称轴为直线x=1,∴抛物线与x轴的另一个交点是(3,0),∴9a+3b+c=0,所以④正确;
∵抛物线与x轴有2个交点,∴b2-4ac>0,所以⑤正确;
故选C.
点评 本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
5. 如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )
如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )
 如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )
如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )| A. | $\sqrt{2}$:1 | B. | 2:1 | C. | 3:1 | D. | 4:1 |
10.若-1<x<0,则x,x2,x3的大小关系是( )
| A. | x<x3<x2 | B. | x<x2<x3 | C. | x3<x<x2 | D. | x2<x3<x |
20.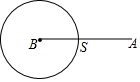 如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )
如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )
 如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )
如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )| A. |  | B. |  | C. | 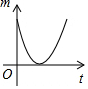 | D. |  |
7.下列实数中是有理数的是( )
| A. | $\sqrt{3}$ | B. | $\root{3}{2}$ | C. | π | D. | π0 |