题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,将点
,将点![]() 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求抛物线的对称轴;
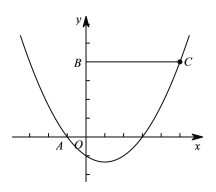
(3)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (5,4);(2)x=1;(3)
(5,4);(2)x=1;(3)![]() 或
或![]() 或
或![]() .
.
【解析】(1)根据直线![]() 与
与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() .即可求出
.即可求出![]() (
(![]() ,0),
,0),![]() (0,4),根据点的平移即可求出点
(0,4),根据点的平移即可求出点![]() 的坐标;
的坐标;
(2)根据抛物线![]() 过
过![]() (
(![]() ,
,![]() ),代入即可求得
),代入即可求得![]() ,根据抛物线的对称轴方程即可求出抛物线的对称轴;
,根据抛物线的对称轴方程即可求出抛物线的对称轴;
(3)分①当抛物线过点![]() 时.②当抛物线过点
时.②当抛物线过点![]() 时.③当抛物线顶点在
时.③当抛物线顶点在![]() 上时.三种情况进行讨论即可.
上时.三种情况进行讨论即可.
(1)解:∵直线![]() 与
与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() .
.
∴![]() (
(![]() ,0),
,0),![]() (0,4)
(0,4)
∴![]() (5,4)
(5,4)
(2)解:抛物线![]() 过
过![]() (
(![]() ,
,![]() )
)
∴![]() .
.![]()
∴![]()
∴对称轴为![]() .
.
(3)解:①当抛物线过点![]() 时.
时.
![]() ,解得
,解得![]() .
.
②当抛物线过点![]() 时.
时.
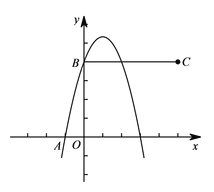
![]() ,解得
,解得![]() .
.
③当抛物线顶点在![]() 上时.
上时.
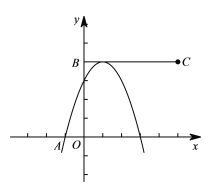
此时顶点为(1,4)
∴![]() ,解得
,解得![]() .
.
∴综上所述![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目