题目内容
6.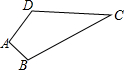 如图,四边形ABCD中,∠A=90°,AB=3,BC=13,CD=12,AD=4,则四边形ABCD的面积等于36.
如图,四边形ABCD中,∠A=90°,AB=3,BC=13,CD=12,AD=4,则四边形ABCD的面积等于36.
分析 连接BD,知四边形的面积是△ADB和△BCD的面积和,由已知得其符合勾股定理的逆定理从而得到△BCD是一个直角三角形.则四边形面积可求.
解答 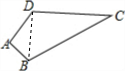 解:连接BD,则有BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
解:连接BD,则有BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵52+122=132,即BD2+CD2=BC2,
∴△BCD为直角三角形,
∴四边形的面积=S△ADB+S△BCD
=$\frac{1}{2}$AD•AB+$\frac{1}{2}$BD•CD
=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12
=36.
故答案为36.
点评 本题利用了勾股定理和它的逆定理及直角三角形的面积公式求解.隐含了整体的数学思想和正确运算的能力.

练习册系列答案
相关题目
 如图,AB,AC是⊙O,D是CA延长线上的一点,AD=AB,∠BDC=25°,则∠BOC=100°.
如图,AB,AC是⊙O,D是CA延长线上的一点,AD=AB,∠BDC=25°,则∠BOC=100°. 如图,分别以五边形的各个顶点为圆心,1cm长为半径作圆,则图中阴影部分的面积为πcm2.
如图,分别以五边形的各个顶点为圆心,1cm长为半径作圆,则图中阴影部分的面积为πcm2. 如图,从?ABCD顶点C向AB和AD的延长线引垂线CE和CF,垂足分别为E、F,求证:AB•AE+AD•AF=AC2.
如图,从?ABCD顶点C向AB和AD的延长线引垂线CE和CF,垂足分别为E、F,求证:AB•AE+AD•AF=AC2.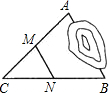 如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=30m,则AB=60m.
如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=30m,则AB=60m.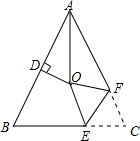 如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为( )
如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为( )