题目内容
如图是一座人行天桥的引桥部分的示意图，上桥通道由两段互相平行并且与地面成37°角的楼梯AD、 BE和一段水平平台DE构成。已知天桥高度BC≈4.8米，引桥水平跨度AC=8米
（1）求水平平台DE的长度；
（2）若与地面垂直的平台立枉MN的高度为3米，求两段楼梯AD与BE的长度之比。
(参考：sin37°=0.60，cos37°=0.80，tan37°=0.75)
（1）1.6米（2）5：3
解析:（1）延长BE交AC于F，∠BFC=∠DAC=37°
则BC/FC=tan37°，∴FC=BC/tan37°=4.8/0.75=6.4米
四边形ADEF为平行四边形，DE=AF=AC-FC=8-6.4=1.6米
（2）过D作DG⊥AC，垂足为G，则DG=MN
DG/AD=sin37°，∴AD=DG/sin37°=3/0.6=5米
BC/BF=sin37°，∴BF=BC/sin37°=4.8/0.6=8米
BE=BF-EF=BE-AD=8-5=3米
∴ AD：BE=5：3
利用解直角三角形求解
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
角的楼梯AD、BE和一段水平平台DE构成．已知天桥高度BC=4.8米，引桥水平跨度AC=8米．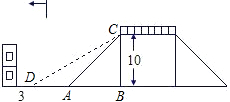
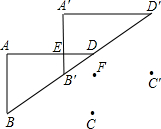
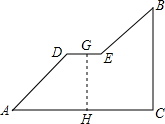如图是一座人行天桥的引桥部分的示意图，上桥通道由两段互相平行并且与地面成37°角的楼梯AD、BE和一段水平平台DE构成．已知天桥高度BC=4.8m，引桥水平跨度AC=8m．
（2009•南安市质检）如图是一座人行天桥的示意图，天桥的高BC为10米，坡面AC的坡角为53°．