题目内容
如图是一座人行天桥的示意图，天桥的高是10米，坡面的倾斜角为45°．为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面的倾斜角为30°，若新坡角下需留3米的人行道，问离原坡角10米的建筑物是否需要拆除？（参考数据：| 2 |
| 3 |
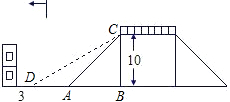
分析：根据坡角利用三角函数分别求得AB，BD的长；从而求得AD的长，然后将AD+3与10进行比较，若大于则需拆除，反之不用拆除．
解答：解：∵∠CAB=45°．
∴AB=BC=10．
∵∠CDB=30°．
∴BD=10
．
∴AD=10
-10≈7.32．（7分）
∵7.32+3＞10．
答：离原坡角10米的建筑物需要拆除．（10分）
解：∵∠CAB=45°．∴AB=BC=10．
∵∠CDB=30°．
∴BD=10
| 3 |
∴AD=10
| 3 |
∵7.32+3＞10．
答：离原坡角10米的建筑物需要拆除．（10分）
点评：此题主要考查学生对坡度坡角的理解及三角函数的运用能力．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
角的楼梯AD、BE和一段水平平台DE构成．已知天桥高度BC=4.8米，引桥水平跨度AC=8米．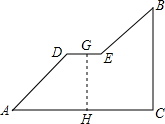
如图是一座人行天桥的引桥部分的示意图，上桥通道由两段互相平行并且与地面成37°角的楼梯AD、BE和一段水平平台DE构成．已知天桥高度BC=4.8m，引桥水平跨度AC=8m．
（2009•南安市质检）如图是一座人行天桥的示意图，天桥的高BC为10米，坡面AC的坡角为53°．