题目内容
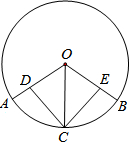 如图,OA、OB是⊙O的半径,点C为弧AB上一点,连接OC.点D、E分别是OA、OB上的点,且AD=BE,连接CD、CE.若CD=CE.求证:∠AOC=∠BOC.
如图,OA、OB是⊙O的半径,点C为弧AB上一点,连接OC.点D、E分别是OA、OB上的点,且AD=BE,连接CD、CE.若CD=CE.求证:∠AOC=∠BOC.考点:全等三角形的判定与性质
专题:
分析:证明∠AOC和∠BOC所在的三角形全等即可.
解答:证明:∵OA=OB AD=BE,
∴OA-AD=OB-BE,
即OD=OE,
在△ODC和△OEC中,
,
∴△ODC≌△OEC(SSS).
∴∠AOC=∠BOC.
∴OA-AD=OB-BE,
即OD=OE,
在△ODC和△OEC中,
|
∴△ODC≌△OEC(SSS).
∴∠AOC=∠BOC.
点评:本题考查了全等三角形的判定和性质以及和圆有关的性质,两条线段或两个角在不同的三角形中要证明相等时,通常是利用全等来进行证明.

练习册系列答案
相关题目
若二次函数y=(m-1)xm2-m的开口向下,则m的值是( )
| A、2 | B、-1 |
| C、2或-1 | D、以上答案都不对 |
下列二次根式中最简二次根式是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法错误的是( )
| A、-1的平方根是±1 |
| B、-1的立方根是-1 |
| C、-1的绝对值是1 |
| D、-1的相反数是1 |
如图所示的图案中,可以由一个“基本图案”连续旋转45°得到的是( )
A、 |
B、 |
C、 |
D、 |