题目内容
5.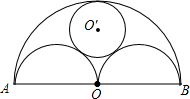 如图.在半圆中,以OA、OB为直径作半圆,⊙O′与三个半圆都相切.若OA=8厘米,求⊙O′的半径.
如图.在半圆中,以OA、OB为直径作半圆,⊙O′与三个半圆都相切.若OA=8厘米,求⊙O′的半径.
分析 如图,作辅助线;设⊙O′的半径为λ;分别表示出O′M、O′O的长;证明O′O⊥MN,运用勾股定理列出关于λ的方程,求出λ即可解决问题.
解答  解:如图,连接O′M、O′N;连接OO′并延长,过切点W.
解:如图,连接O′M、O′N;连接OO′并延长,过切点W.
设⊙O′的半径为λ;
∵⊙O′与⊙M、⊙N两两外切,
∴O′M=O′N=λ+4,O′O=8-λ;
∵OM=ON,
∴O′O⊥MN;由勾股定理得:
(λ+4)2=42+(8-λ)2,
解得:λ=$\frac{8}{3}$(cm).
点评 该题主要考查了相切两圆的性质、勾股定理等几何知识点及其应用问题;解题的关键是作辅助线,构造直角三角形,灵活运用相切两圆的性质等几何知识点来分析、解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.如果两条不同的直线都和第三条直线平行,那么这两条直线的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 平行或相交 | D. | 互相垂直 |
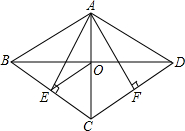 如图 在?ABCD中 对角线AC、BD 相交于点O,AE⊥BC,AF⊥CD,垂足分别是E、F,点E、F恰好为BC、CD的中点,连接OE.
如图 在?ABCD中 对角线AC、BD 相交于点O,AE⊥BC,AF⊥CD,垂足分别是E、F,点E、F恰好为BC、CD的中点,连接OE.