题目内容
 如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边且在CD的下方作等边△CDE,连结BE.
如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边且在CD的下方作等边△CDE,连结BE.(1)填空:∠ACB=
60
60
度;(2)当点D在线段AM上(点D不运动到点A)时,试求出
| AD | BE |
分析:(1)根据等边三角形的三个内角都是60°进行填空;
(2)通过全等三角形的判定定理SAS证得△ACD≌△BCE,则对应边相等:AD=BE,所以
=1.
(2)通过全等三角形的判定定理SAS证得△ACD≌△BCE,则对应边相等:AD=BE,所以
| AD |
| BE |
解答:解:(1)∵△ABC是等边三角形,
∴∠ACB=60°.
(2)∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,
∠ACB=∠DCE=60°
∴∠ACD+∠DCB=∠DCB+∠BCE
∴∠ACD=∠BCE
在△ACD与△BCE中,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∴
=1.
故答案是:60.

∴∠ACB=60°.
(2)∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,
∠ACB=∠DCE=60°
∴∠ACD+∠DCB=∠DCB+∠BCE
∴∠ACD=∠BCE
在△ACD与△BCE中,
|
∴△ACD≌△BCE(SAS),
∴AD=BE,
∴
| AD |
| BE |
故答案是:60.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
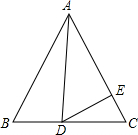 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
 16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是
16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°. 如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.
如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: