题目内容
19. 如图,在半径为5的⊙O中,弦AB=8,OP⊥AB,垂足为点P,则OP的长为( )
如图,在半径为5的⊙O中,弦AB=8,OP⊥AB,垂足为点P,则OP的长为( )| A. | 4 | B. | 5 | C. | 3 | D. | 2 |
分析 连接OA,根据垂径定理求出AP,根据勾股定理求出OP即可.
解答 解:
连接OA,则OA=5,
∵OP⊥AB,AB=8,OP过O,
∴AP=BP=$\frac{1}{2}$AB=4,
在Rt△OAP中,由勾股定理得:OP=$\sqrt{O{A}^{2}-A{P}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
故选C.
点评 本题考查了垂径定理和勾股定理,能根据垂径定理得出AP=BP是解此题的关键,注意:垂直于弦的直径平分这条弦.

练习册系列答案
相关题目
9. 如图,AB∥CD,∠DCE=75°,则∠BEF=( )
如图,AB∥CD,∠DCE=75°,则∠BEF=( )
 如图,AB∥CD,∠DCE=75°,则∠BEF=( )
如图,AB∥CD,∠DCE=75°,则∠BEF=( )| A. | 105° | B. | 95° | C. | 80° | D. | 75° |
10.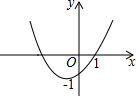 如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,-1),且顶点在第三象限,则a的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,-1),且顶点在第三象限,则a的取值范围是( )
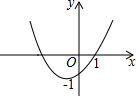 如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,-1),且顶点在第三象限,则a的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,-1),且顶点在第三象限,则a的取值范围是( )| A. | a>0 | B. | 0<a<1 | C. | 1<a<2 | D. | -1<a<1 |
7.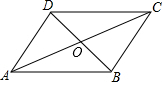 如图,下列哪组条件能判定四边形ABCD是平行四边形( )
如图,下列哪组条件能判定四边形ABCD是平行四边形( )
 如图,下列哪组条件能判定四边形ABCD是平行四边形( )
如图,下列哪组条件能判定四边形ABCD是平行四边形( )| A. | AB∥CD,AD=BC | B. | AB=AD,CB=CD | ||
| C. | ∠DAB=∠ABC,∠BCD=∠CDA | D. | AO=CO,BO=DO |
14.下列是二元一次方程的是( )
| A. | 3x-6y=xy | B. | 3x-6=x | C. | 3x-$\frac{6}{y}$=0 | D. | 3x-6y=x |
4.2014年“双十一”淘宝商城销售额达到571亿元,2016年上升至1207亿元.设这两年的平均增长率为x,则下列方程正确的是( )
| A. | 571(1+x)=1207 | B. | 571(1+2x)=1207 | ||
| C. | 571(1+x)2=1207 | D. | 571(1+x)+350(1+x)2=1207 |
11.下列各数中是无理数的是( )
| A. | $\sqrt{4}$ | B. | $\frac{22}{7}$ | C. | $\frac{π}{2}$ | D. | 1.010010001 |
2.吋是电视机常用规格之一,1吋约为拇指上面一节的长,则4吋长相当于( )
| A. | 课本的宽度 | B. | 粉笔的长度 | C. | 课桌的宽度 | D. | 黑板的高度 |