题目内容
 (1997•南京)如图,正六边形的螺帽的边长为a,这个搬手的开口b最小应是(用含a的代数式表示)( )
(1997•南京)如图,正六边形的螺帽的边长为a,这个搬手的开口b最小应是(用含a的代数式表示)( )分析:首先取此正六边形的中心O,连接OC,OD,过点O作OH⊥CD于点H,易求得OH的长,继而求得这个搬手的开口b最小值.
解答: 解:取此正六边形的中心O,连接OC,OD,过点O作OH⊥CD于点H,
解:取此正六边形的中心O,连接OC,OD,过点O作OH⊥CD于点H,
则∠COD=60°,
∴∠COH=
∠COD=30°,CH=DH=
CD=
a,
∴OC=2CH=a,
在Rt△OCH中,OH=
=
a,
∴b=2OH=
a.
故选A.
 解:取此正六边形的中心O,连接OC,OD,过点O作OH⊥CD于点H,
解:取此正六边形的中心O,连接OC,OD,过点O作OH⊥CD于点H,则∠COD=60°,
∴∠COH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OC=2CH=a,
在Rt△OCH中,OH=
| OC2-CH2 |
| ||
| 2 |
∴b=2OH=
| 3 |
故选A.
点评:此题考查了正多边形与圆的知识.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 (1997•南京)如图,在?ABCD中,E是BC中点,F是BE中点,AE与DF交于点H,则S△EFH与S△ADH的比值是( )
(1997•南京)如图,在?ABCD中,E是BC中点,F是BE中点,AE与DF交于点H,则S△EFH与S△ADH的比值是( ) (1997•南京)已知如图,在△ABC的外接圆中,D是弧BC的中点,AD交BC于点E,∠ABC的平分线交AD于点F.
(1997•南京)已知如图,在△ABC的外接圆中,D是弧BC的中点,AD交BC于点E,∠ABC的平分线交AD于点F.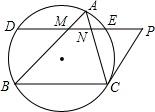 (1997•南京)已知:如图,△ABC内接于⊙O,P为⊙O外一点,作∠CPD=∠A,使PD交⊙O于D、E两点,并与AB、AC分别交于点M、N.
(1997•南京)已知:如图,△ABC内接于⊙O,P为⊙O外一点,作∠CPD=∠A,使PD交⊙O于D、E两点,并与AB、AC分别交于点M、N. (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.