题目内容
20．
含30°角的直角三角板与直线l1、l2的位置关系如图所示，已知l1∥l2，∠ACD=∠A，则∠1=（ ）| A． | 70° | B． | 60° | C． | 40° | D． | 30° |
分析 先根据三角形外角性质得到∠CDB的度数，再根据平行线的性质，即可得到∠1的度数．
解答 解：∵∠ACD=∠A=30°，
∴∠CDB=∠A+∠ACD=60°，
∵l1∥l2，
∴∠1=∠CDB=60°，
故选：B．
点评 本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，内错角相等．
练习册系列答案
相关题目
10．
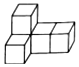有5个大小相同的小正方体，它们的棱长为1，将这5个正方体拼成如图所示的几何体，则下列说法正确的是（ ）
有5个大小相同的小正方体，它们的棱长为1，将这5个正方体拼成如图所示的几何体，则下列说法正确的是（ ）| A． | 主视图的面积为3 | B． | 左视图的面积为3 | ||
| C． | 俯视图的面积为5 | D． | 三个视图的面积相等 |
如图，在6×10正方形网格中，每个小正方形的边长为1个单位长度，作△ABC关于点O的中心对称图形△A′B′C′．
8．
如图，在⊙O中，AB是⊙O的弦，点C是优弧$\widehat{AB}$上一点，连接OA、OC．若∠AOC=100°，则∠B的度数为（ ）
如图，在⊙O中，AB是⊙O的弦，点C是优弧$\widehat{AB}$上一点，连接OA、OC．若∠AOC=100°，则∠B的度数为（ ）| A． | 150° | B． | 130° | C． | 100° | D． | 50° |
15．
如图，下列条件中不能判定AB∥CD的是（ ）
如图，下列条件中不能判定AB∥CD的是（ ）| A． | ∠3=∠4 | B． | ∠1=∠5 | C． | ∠1+∠4=180° | D． | ∠3=∠5 |
12．下列说法正确的是（ ）
| A． | 要了解某公司生产的100万只灯泡的使用寿命，可以采用抽样调查的方法 | |
| B． | 4位同学的数学期末成绩分别为100、95、105、110，则这四位同学数学期末成绩的中位数为100 | |
| C． | 甲乙两人各自跳远10次，若他们跳远成绩的平均数相同，甲乙跳远成绩的方差分别为0.51和0.62 | |
| D． | 某次抽奖活动中，中奖的概率为$\frac{1}{50}$表示每抽奖50次就有一次中奖 |
9．对于函数y=-2（x-m）2的图象，下列说法不正确的是（ ）
| A． | 开口向下 | B． | 对称轴是x=m | C． | 最大值为0 | D． | 与y轴不相交 |
17．下列计算正确的是（ ）
| A． | （a2）3=a5 | B． | a-2•a2=a-4 | C． | 3$\sqrt{5}$-$\sqrt{5}$=3 | D． | $\sqrt{9}$=3 |