题目内容
如图,在平面直角坐标系中,直线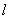 ∥x轴,且直线
∥x轴,且直线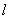 分别与反比例函数y=
分别与反比例函数y=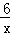 (x>0)和y=﹣
(x>0)和y=﹣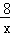 (x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
(x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
7

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
题目内容
如图,在平面直角坐标系中,直线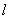 ∥x轴,且直线
∥x轴,且直线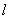 分别与反比例函数y=
分别与反比例函数y=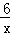 (x>0)和y=﹣
(x>0)和y=﹣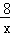 (x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
(x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
7

 全能闯关100分系列答案
全能闯关100分系列答案