��Ŀ����
����Ŀ�����عˡ�
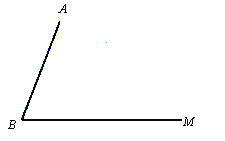
��ͼ1����ABC�У���B=30����AB=3��BC=4������ABC��������� ��
��̽����
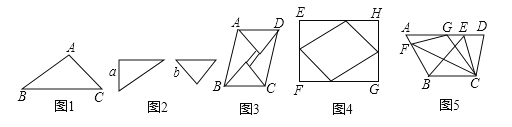
ͼ2��ͬѧ����Ϥ��һ�����dzߣ�һ������30���Ľǣ��϶̵�ֱ�DZ߳�Ϊa����һ������45���Ľǣ�ֱ�DZ߳�Ϊb��С�����������������dz�ƴ��һ��ƽ���ı���ABCD����ͼ3�����������ֲ�ͬ�ķ�����������������Ӷ��Ƴ�sin75��=![]() ��С�����������������dz�ƴ����һ������EFGH����ͼ4����Ҳ�Ƴ�sin75��=
��С�����������������dz�ƴ����һ������EFGH����ͼ4����Ҳ�Ƴ�sin75��=![]() ������д��С����С���Ƴ�sin75��=
������д��С����С���Ƴ�sin75��=![]() �ľ���˵�����̣�
�ľ���˵�����̣�
��Ӧ�á�
���ı���ABCD�У�AD��BC����D=75����BC=6��CD=5��AD=10����ͼ5����
��1����E��AD�ϣ���t=BE+CE����t2����Сֵ��
��2����F��AB�ϣ�����BCF��CF���ۣ���B����AD�ϵĵ�G������G��AD���е���˵�����ɣ�
���𰸡����عˡ�3����̽�����𰸼���������Ӧ�á���1��86+25![]() ����2����G����AD���е㣮
����2����G����AD���е㣮
������������������عˣ���ͼ1�У���AH��BC�����AH���ɽ�����⣻
̽������ͼ2�У�����S�ı���ABCD=BCABsin75��=2S��ABE+2S��BFC+S����EFGH�г����̼��ɽ�����⣻
Ӧ�ã���1����C����AD�ĶԳƵ�H��CH��AD��J������BH��EH����ΪEC=EH���Ƴ�EB+EC=EB+EH������EBH�У�BE+EH��BH���Ƴ�BE+EC����СֵΪBH�����BH���ɽ�����⣻
��2�����ۣ���G����AD���е㣮���ɷ�֤��֤�����ɣ�
����������⣺�������֪�ı���EFGH�Ǿ��Σ�AB=CD=2a��AH=DH=BF=CF=b��EF=GH=![]() a��b��EH=FG=b��a��BC=
a��b��EH=FG=b��a��BC=![]() b��
b��
���ع�����ͼ1�У���AH��BC��
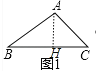
��Rt��ABH�У��ߡ�B=30����AB=3����AH=ABsin30��=![]() ����S��ABC=
����S��ABC=![]() BCAH=
BCAH=![]() ��4��
��4��![]() =3���ʴ�Ϊ��3��
=3���ʴ�Ϊ��3��
̽������ͼ3�У�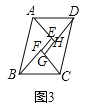
�������֪�ı���EFGH�Ǿ��Σ�AB=CD=2a��AH=DH=BF=CF=b��EF=GH=![]() a��b��EH=FG=b��a��BC=
a��b��EH=FG=b��a��BC=![]() b����S�ı���ABCD=BCABsin75��=2S��ABE+2S��BFC+S����EFGH
b����S�ı���ABCD=BCABsin75��=2S��ABE+2S��BFC+S����EFGH
��![]() b2asin75��=2��
b2asin75��=2��![]() ��a��
��a��![]() a+2��
a+2��![]() ��b2+��
��b2+��![]() a��b����b��a������2
a��b����b��a������2![]() absin75��=
absin75��=![]() ab+ab����sin75��=
ab+ab����sin75��=![]() ��
��
��ͼ4�У�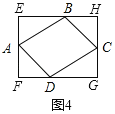
��֪�ı���ABCD��ƽ���ı��Σ���BAD=75������S�ı���EFGH=2S��ABE+2S��ADF+Sƽ���ı���ABCD������a+b����![]() a+b���T2��
a+b���T2��![]() ��a��
��a��![]() a+2��
a+2��![]() ��b2+
��b2+![]() b2asin75������sin75��=
b2asin75������sin75��=![]() ��
��
Ӧ�ã���1����C����AD�ĶԳƵ�H��CH��AD��J������BH��EH��
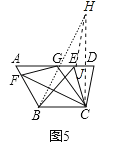
��Rt��DCJ��JC=CDsin75��=![]() ����CH=2CJ=
����CH=2CJ=![]() ����Rt��BHC��BH2=BC2+CH2=36+
����Rt��BHC��BH2=BC2+CH2=36+![]() =86+25
=86+25![]() ����EC=EH����EB+EC=EB+EH������EBH�У�BE+EH��BH����BE+EC����СֵΪBH����t=BE+CE��t2����СֵΪBH2����Ϊ86+25
����EC=EH����EB+EC=EB+EH������EBH�У�BE+EH��BH����BE+EC����СֵΪBH����t=BE+CE��t2����СֵΪBH2����Ϊ86+25![]() ��
��
��2�����ۣ���G����AD���е㣮
���ɣ���CJ��AD��J��DH��CG��H��
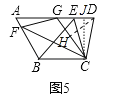
������AG=GD=5����CD=5����DC=DG����DH��CG����GH=CH=3����Rt��CDH��DH=![]() =
=![]() =4����S��DGC=
=4����S��DGC=![]() CGDH=
CGDH=![]() DGCJ����CJ=
DGCJ����CJ=![]() ����sin��CDJ=
����sin��CDJ=![]() ���ߡ�CDJ=75��������sin75��=
���ߡ�CDJ=75��������sin75��=![]() ì�ܣ������費����������G����AD���е㣮
ì�ܣ������費����������G����AD���е㣮

 ��У����ϵ�д�
��У����ϵ�д�