Question

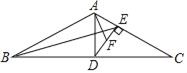
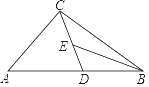
【题目】如图，在△ABC中，D为AB边上一点，E为CD中点，AC=，∠ABC=30°，∠A=∠BED=45°，则BD的长为（ ）．

A.B.C.D.

Answer 1

【答案】D

【解析】

根据题意过C作CF⊥AB于F，过点B作BG⊥CD于G，并设DF=x，CE=DE=y，利用相似三角形的性质以及解直角三角形相关进行分析计算即可.

解：如图，过C作CF⊥AB于F，过点B作BG⊥CD于G，

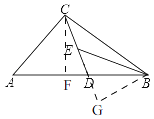
在Rt△BEG中，∠BED=45°，则GE=GB．

在Rt△AFC中，∠A=45°，AC=，则AF=CF=×sin45°=1，

在Rt△BFC中，∠ABC=30°，CF=1，则BC=2CF=2，BF=CF=，

设DF=x，CE=DE=y，则BD=-x，

∴△CDF∽△BDG，

∴==，

∴==，

∴DG=，BG=，

∵GE=GB，

∴y+=，

∴2y2+x(﹣x)=﹣x，

在Rt△CDF中，

∵CF2+DF2=CD2，

∴1+x2=4y2，

∴+x(﹣x)=﹣x，

整理得：x2﹣(2+2)x+2﹣1=0，

解得x=1+-或1+-(舍弃)，

∴BD=-x=-1．

故答案为：D．