Question

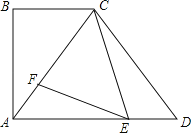
【题目】如图，直径为10的⊙O经过原点O，并且与x轴、y轴分别交于A、B两点，线段OA、OB（OA＞OB）的长分别是方程x2+kx+48=0的两根．

（1）求线段OA、OB的长；

（2）已知点C在劣弧OA上，连结BC交OA于D，当OC2=CD·CB时，求C点的坐标；

（3）在⊙O上是否存在点P，使S△POD=S△ABD．若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）OA=8，OB=6；（2）C（4，-2）；（3）不存在，理由见解析．

【解析】

（1）根据根与系数的关系写出OA+OB和OAOB的值．连接AB，根据90°的圆周角所对的弦是直径，再结合勾股定理列方程求解．

（2）若OC2=CDCB，则三角形OCB相似于三角形DCO，则∠COD=∠CBO．又∠COD=∠CBA，则∠CBO=∠CBA，所以点C是弧OA的中点．连接O′C，根据垂径定理的推论，得O′E⊥OA．再进一步根据垂径定理和勾股定理进行计算即可．

（3）首先求得直线BC的解析式，求得D的坐标，根据面积相等即可求得P的纵坐标，根据圆的直径即可作出判断．

解：（1）连接AB，∵∠BOA=90°，

∴AB为直径，根与系数关系得OA+OB=-k，OAOB=48；

根据勾股定理，得OA2+OB2=100，

即（OA+OB）2-2OAOB=100，

解得k2=196，∴k=±14（正值舍去）．

则有方程x2-14x+48=0，x=6或8．

又OA＞OB，

∴OA=8，OB=6．

（2）若OC2=CD×CB，则△OCB∽△DCO，

∴∠COD=∠CBO，

又∵∠COD=∠CBA，

∴∠CBO=∠CBA，

所以点C是弧OA的中点．

连接O′C交OA于点D，根据垂径定理的推论，得O′C⊥OA，

根据垂径定理，得OD=4，

根据勾股定理，得O′D=3，

∴CD=2，即C（4，-2）．

（3）设直线BC的解析式是y=kx+b，把B（0,6）,C（4,-2）代入

解得：K=-2,b=6

则直线BC的解析式是y=-2x+6，

令y=0，解得：x=3，

则OD=3，AD=8-3=5，

∴S△ABD=×5×6=15．

若S△ABD=S△OBD，P到x轴的距离是h，

则×3h=15，解得：h=10．

而⊙O′的直径是10，因而P不能在⊙O′上，

故P不存在．