��Ŀ����
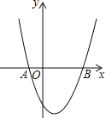
����Ŀ��ij��˾2017����ճ���ʱͶ��1000��Ԫ�����������������²�Ʒ�����⣬����ÿ���ò�Ʒ����Ҫ�ɱ�40Ԫ.���涨���ò�Ʒ�ۼ۲��õ���60Ԫ/���Ҳ�����160Ԫ/������ÿ���ۼ�ȷ���Ժ��ٱ仯���ò�Ʒ����������![]() ����������Ʒ�ۼ�
����������Ʒ�ۼ�![]() ��Ԫ��֮��ĺ�����ϵ��ͼ��ʾ��
��Ԫ��֮��ĺ�����ϵ��ͼ��ʾ��
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ����д��
֮��ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����2017��ù�˾���������
��3����2017��ȡ����������ǰ���£�2018�깫˾������ȷ����Ʒ�ۼۣ��ܷ�ʹ���깲ӯ����980��Ԫ.���ܣ����2018���Ʒ���ۼۣ������ܣ���˵�����ɣ�

���𰸡���1��![]() ����2��
����2��![]() ��Ԫ����3���ܣ��ۼ�Ϊ100Ԫ/��.
��Ԫ����3���ܣ��ۼ�Ϊ100Ԫ/��.
��������
��1����y=kx+b������ͼ������k��b���Ӷ��ó�y��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ60��x��160��
��2���蹫˾��һ�����W��Ԫ����ɱ�ʾ��W=-![]() ��x-160��2+200����2017��ù�˾���������200��Ԫ��
��x-160��2+200����2017��ù�˾���������200��Ԫ��
��3��980-200=780��Ԫ����x-40����![]() ��=780�����x1=100��x2=300����2018������Ϊ780��Ԫ.
��=780�����x1=100��x2=300����2018������Ϊ780��Ԫ.
�⣺��1����y=kx+b������ͼ��֪��![]()
���k=![]() ��b=18����
��b=18����![]() .
.
��2���蹫˾1017�����W��Ԫ��
��W=��x-40��y-1000=��x-40����![]() ��-100= W=-
��-100= W=-![]() ��x-160��2+200
��x-160��2+200
��3��980-200=780��Ԫ����2018������Ϊ780��Ԫ.
��x-40����![]() ��=780�����x1=100��x2=300�����������⣬��ȥ��
��=780�����x1=100��x2=300�����������⣬��ȥ��
���ܣ��ۼ�Ϊ100Ԫ/��.

 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�