题目内容
6.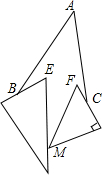 如图,已知两块三角板如图摆放,点B和点C分别在两块三角板的边上,一块三角板的顶点M在另一块三角板的边上,且∠BAC=40°,∠E=60°,∠F=45°,则∠ABE+∠EMF+∠FCA=65 度.
如图,已知两块三角板如图摆放,点B和点C分别在两块三角板的边上,一块三角板的顶点M在另一块三角板的边上,且∠BAC=40°,∠E=60°,∠F=45°,则∠ABE+∠EMF+∠FCA=65 度.
分析 延长BE交AC于D,延长CF交BD于G,根据外角的性质得到∠EGF=∠BDC+∠ACF=∠A+∠ABE+∠ACF,根据四边形的内角和和邻补角的定义得到∠ABE+∠EMF+∠FCA+∠A=∠BEM+∠CFM=105°,于是得到结论.
解答  解:延长BE交AC于D,延长CF交BD于G,
解:延长BE交AC于D,延长CF交BD于G,
∵∠BDC=∠A+∠ABE,
∠EGF=∠BDC+∠ACF=∠A+∠ABE+∠ACF,
∴∠ABE+∠EMF+∠FCA+∠A=∠BEM+∠CFM=105°,
∴∠ABE+∠EMF+∠FCA=105°-∠A=65°,
故答案为:65.
点评 本题考查了三角形的外角的性质,四边形的内角和,邻补角的定义,熟练掌握三角形的外角的性质是解题的关键.

练习册系列答案
相关题目
17.已知a>b,且c为非零实数,那么下列结论一定正确的是( )
| A. | ac<bc | B. | ac2<bc2 | C. | ac>bc | D. | ac2>bc2 |
14.宁波奥林匹克体育中心坐落于江北区,一期“三馆一圆”总投资35亿元,其中35亿元用科学记数法表示为( )
| A. | 0.35×1010元 | B. | 3.5×108元 | C. | 3.5×109元 | D. | 35×108元 |
1. 一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据(如表)
一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据(如表)
为观察s与t之间的关系,建立坐标系(如图),以t为横坐标,s为纵坐标,请描出表中数据对应的5个点,并用平滑曲线连接它们,再根据这条曲线图象,利用我们所学的函数,近似地表示s关于t的函数关系式.
 一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据(如表)
一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据(如表)| 滑行时间t/s | 0 | 1 | 2 | 3 | 4 |
| 滑行距离s/m | 0 | 4.5 | 14 | 28.5 | 48 |
15.下列图形中,不是正方体平面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
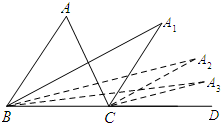 如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2013为$\frac{α}{{2}^{2012}}$.
如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2013为$\frac{α}{{2}^{2012}}$. 如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F.
如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F.