题目内容
 把矩形OABC放在平面直角坐标系中,OA,OC分别放在x轴、y轴的正半轴上,O为坐标原点,已知OA=4,OC=2,沿直线OB将△OAB翻折,点A落在该平面直角坐标系中的D处,则经过D点的双曲线的解析式为________.
把矩形OABC放在平面直角坐标系中,OA,OC分别放在x轴、y轴的正半轴上,O为坐标原点,已知OA=4,OC=2,沿直线OB将△OAB翻折,点A落在该平面直角坐标系中的D处,则经过D点的双曲线的解析式为________.
y=
分析:设D(x,y),连AD,与OB交于E,作DF⊥OA,由面积法可求得AE的长,在Rt△ODF和Rt△DFA中,由勾股定理知:DF=OD2-OF2=AD2-AF2,解得x的值,再求得y的值即可.
解答: 解:连AD,与OB交于E,作DF⊥OA,
解:连AD,与OB交于E,作DF⊥OA,
∵OA=OD,∠AOE=∠DOE,
∴△AOD是等腰三角形,OE是AD边上的高,
∴AE=DE,AD=2AE,
AE= =
= ,
,
设D(x,y),则有:OD2-OF2=AD2-AF2,即:
42-x2=(2AE)2-(4-x)2,
解得:x= ,
,
y=DF= ,
,
∴D点的坐标为:( ,
, ),
),
设y= ,
,
得k=x×y=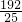 ,
,
∴y= .
.
故本题答案为:y= .
.
点评:本题考查了坐标与图形的性质,矩形的性质以及勾股定理等的运用.

分析:设D(x,y),连AD,与OB交于E,作DF⊥OA,由面积法可求得AE的长,在Rt△ODF和Rt△DFA中,由勾股定理知:DF=OD2-OF2=AD2-AF2,解得x的值,再求得y的值即可.
解答:
 解:连AD,与OB交于E,作DF⊥OA,
解:连AD,与OB交于E,作DF⊥OA,∵OA=OD,∠AOE=∠DOE,
∴△AOD是等腰三角形,OE是AD边上的高,
∴AE=DE,AD=2AE,
AE=
 =
= ,
,设D(x,y),则有:OD2-OF2=AD2-AF2,即:
42-x2=(2AE)2-(4-x)2,
解得:x=
 ,
,y=DF=
 ,
,∴D点的坐标为:(
 ,
, ),
),设y=
 ,
,得k=x×y=
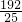 ,
,∴y=
 .
.故本题答案为:y=
 .
.点评:本题考查了坐标与图形的性质,矩形的性质以及勾股定理等的运用.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 9、如图,矩形OABC放在平面直角坐标系中,OC=2,OA=4,将矩形OABC绕原点O按顺时针方向旋转90°得到矩形OA′B′C′,则点B′的坐标是
9、如图,矩形OABC放在平面直角坐标系中,OC=2,OA=4,将矩形OABC绕原点O按顺时针方向旋转90°得到矩形OA′B′C′,则点B′的坐标是 把矩形OABC放在平面直角坐标系中,OA,OC分别放在x轴、y轴的正半轴上,O为坐标原点,已知OA=4,OC=2,沿直线OB将△OAB翻折,点A落在该平面直角坐标系中的D处,则经过D点的双曲线的解析式为
把矩形OABC放在平面直角坐标系中,OA,OC分别放在x轴、y轴的正半轴上,O为坐标原点,已知OA=4,OC=2,沿直线OB将△OAB翻折,点A落在该平面直角坐标系中的D处,则经过D点的双曲线的解析式为 如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为( )
如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为( )