题目内容
20.已知二次函数y=ax2-4x+1的图象与x轴的两个交点,则a的取值范围是a<4且a≠0.分析 根据二次函数y=ax2-4x+1的图象与x轴有两个公共点可知△>0且a≠0,据此可知a的取值范围.
解答 解:∵二次函数y=ax2-4x+1的图象与x轴有两个公共点,
∴△>0且a≠0,
即16-4a>0,
解得a<4且a≠0.
故答案是:a<4且a≠0.
点评 本题考查了二次函数的定义和抛物线与x轴的交点,要结合判别式进行解答.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
11.肖丽去商店买练习本,回来后告诉同学们:“店主给我说,如果多买一些就给我8折优惠,所以我就买了20本,结果便宜了4.8元.”如果设原来每本练习本价格为x元,则根据题意所列方程错误的是( )
| A. | 20(1-0.8)x=4.8 | B. | 20x-20×0.8x=4.8 | C. | 20x=20×0.8x+4.8 | D. | 20×0.8x=4.8 |
5.“三次投掷一枚硬币,三次正面朝上”这一事件是( )
| A. | 必然事件 | B. | 随机事件 | C. | 不可能事件 | D. | 确定事件 |
12.矩形ABCD的长AD=15cm,宽AB=10cm,∠ABC的平分线分AD边为AE、ED两部分,这AE、ED的长分别为( )
| A. | 11cm和4cm | B. | 10cm和5cm | C. | 9cm和6cm | D. | 8cm和7cm |
9.在△ABC和△A'B'C'中,已知∠A=∠A′,∠B=∠B',AB=A'B',那么△ABC≌△A′B′C′运用的判定方法是( )
| A. | SAS | B. | AAS | C. | ASA | D. | SSS |
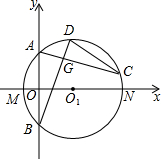 如图,在平面直角坐标系中,直线y=2x+4交x轴于点M,交y轴于点A,过A,M两点的⊙O1的圆心O1在x轴上,交x轴于另一点N,交y轴于另一点B,D,C为优弧$\widehat{AB}$上两动点,且AC⊥BD交BD于G,延长OG交CD于H.
如图,在平面直角坐标系中,直线y=2x+4交x轴于点M,交y轴于点A,过A,M两点的⊙O1的圆心O1在x轴上,交x轴于另一点N,交y轴于另一点B,D,C为优弧$\widehat{AB}$上两动点,且AC⊥BD交BD于G,延长OG交CD于H.