题目内容
若a,b,c是实数,且a=2b+ ,ab+
,ab+ c2+
c2+ =0,那么
=0,那么 的值是________.
的值是________.
0
分析:将a=2b+ 代入ab+
代入ab+ c2+
c2+ =0中,利用配方法将等式变形为两个非负数的和为0的形式,利用几个非负数的和为0,这几个非负数都为0,解答本题.
=0中,利用配方法将等式变形为两个非负数的和为0的形式,利用几个非负数的和为0,这几个非负数都为0,解答本题.
解答:解法一:
将a=2b+ 代入ab+
代入ab+ c2+
c2+ =0中,得
=0中,得
ab+ c2+
c2+ =(2b+
=(2b+ )b+
)b+ c2+
c2+
=[( b)2+2(
b)2+2( b)•
b)• +(
+( )2]+
)2]+ c2
c2
=( b+
b+ )2+
)2+ c2=0,
c2=0,
∴c=0,b=-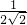 ,即
,即 =0.
=0.
解法二:
∵a=2b+ ,
,
∴a-2b=
两边平方,得a2-4ab+4b2=2 ①
又ab+ c2+
c2+ =0,得出
=0,得出
8ab+4 c2=-2 ②
c2=-2 ②
①+②得:a2+4ab+4b2+4 c2=0,
c2=0,
即(a+2b)2+4 c2=0
c2=0
∴a+2b=0,c=0,
则 =0.故答案为0.
=0.故答案为0.
点评:本题考查了配方法在等式变形中的运用,非负数的性质,需要熟练掌握.
分析:将a=2b+
 代入ab+
代入ab+ c2+
c2+ =0中,利用配方法将等式变形为两个非负数的和为0的形式,利用几个非负数的和为0,这几个非负数都为0,解答本题.
=0中,利用配方法将等式变形为两个非负数的和为0的形式,利用几个非负数的和为0,这几个非负数都为0,解答本题.解答:解法一:
将a=2b+
 代入ab+
代入ab+ c2+
c2+ =0中,得
=0中,得ab+
 c2+
c2+ =(2b+
=(2b+ )b+
)b+ c2+
c2+
=[(
 b)2+2(
b)2+2( b)•
b)• +(
+( )2]+
)2]+ c2
c2=(
 b+
b+ )2+
)2+ c2=0,
c2=0,∴c=0,b=-
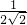 ,即
,即 =0.
=0.解法二:
∵a=2b+
 ,
,∴a-2b=

两边平方,得a2-4ab+4b2=2 ①
又ab+
 c2+
c2+ =0,得出
=0,得出8ab+4
 c2=-2 ②
c2=-2 ②①+②得:a2+4ab+4b2+4
 c2=0,
c2=0,即(a+2b)2+4
 c2=0
c2=0∴a+2b=0,c=0,
则
 =0.故答案为0.
=0.故答案为0.点评:本题考查了配方法在等式变形中的运用,非负数的性质,需要熟练掌握.

练习册系列答案
相关题目
若a、b、c是实数,a≠0,ax3+bx2-c的一个因式是x2+2x-1,则
等于( )
| b |
| a |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
 ,
, =4则
=4则 =________.
=________.