题目内容
15.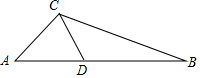 经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为113°或92°.
经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为113°或92°.
分析 由△ACD是等腰三角形,∠ADC>∠BCD,推出∠ADC>∠A,即AC≠CD,分两种情形讨论①当AC=AD时,②当DA=DC时,分别求解即可.
解答 解: ∵△BCD∽△BAC,
∵△BCD∽△BAC,
∴∠BCD=∠A=46°,
∵△ACD是等腰三角形,∵∠ADC>∠BCD,
∴∠ADC>∠A,即AC≠CD,
①当AC=AD时,∠ACD=∠ADC=$\frac{1}{2}$(180°-46°)=67°,
∴∠ACB=67°+46°=113°,
②当DA=DC时,∠ACD=∠A=46°,
∴∠ACB=46°+46°=92°,
故答案为113°或92°.
点评 本题考查相似三角形的性质、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
5.云南某特产公司组织20辆汽车装运三七、普洱茶、鲜花饼三种特产去省外销售,按计划20辆汽车都要装运,每辆汽车只能运送同一种特产,且必须装满,根据下表提供的信息,解答以下问题;
若装运三七的车辆数为x,装运鲜花饼的车辆数比装运三七的车辆数的2倍少1辆,假设三种特产的总利润为y万元.
(1)求y与x的函数关系式;
(2)若装运普洱茶的汽车不超过6辆,求总利润最大时,装运各种特产的车辆数及总利润最大值.
| 特产名称 | 三七 | 普洱茶 | 鲜花饼 |
| 每辆汽车运载量(吨) | 8 | 6 | 5 |
| 每吨特产利润(万元) | 1.2 | 1.6 | 1 |
(1)求y与x的函数关系式;
(2)若装运普洱茶的汽车不超过6辆,求总利润最大时,装运各种特产的车辆数及总利润最大值.
6. 五个大小相同的正方体搭成的几何体如图所示,其左视图是( )
五个大小相同的正方体搭成的几何体如图所示,其左视图是( )
 五个大小相同的正方体搭成的几何体如图所示,其左视图是( )
五个大小相同的正方体搭成的几何体如图所示,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
10.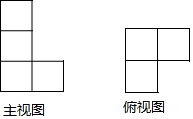 一个几何体的主视图和俯视图如图所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b等于( )
一个几何体的主视图和俯视图如图所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b等于( )
 一个几何体的主视图和俯视图如图所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b等于( )
一个几何体的主视图和俯视图如图所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b等于( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
20.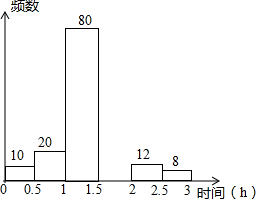 为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动.某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动.某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
(1)表中a=70,b=0.40;
(2)请补全频数分布直方图中空缺的部分;
(3)样本中,学生日阅读所用时间的中位数落在第3组;
(4)请估计该校七年级学生日阅读量不足1小时的人数.
 为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动.某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动.某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:(1)表中a=70,b=0.40;
(2)请补全频数分布直方图中空缺的部分;
(3)样本中,学生日阅读所用时间的中位数落在第3组;
(4)请估计该校七年级学生日阅读量不足1小时的人数.
| 组别 | 时间段(小时) | 频数 | 频率 |
| 1 | 0≤x<0.5 | 10 | 0.05 |
| 2 | 0.5≤x<1.0 | 20 | 0.10 |
| 3 | 1.0≤x<1.5 | 80 | b |
| 4 | 1.5≤x<2.0 | a | 0.35 |
| 5 | 2.0≤x<2.5 | 12 | 0.06 |
| 6 | 2.5≤x<3.0 | 8 | 0.04 |
4.下列运算正确的是( )
| A. | a3+a2=a5 | B. | a3÷a2=a | C. | a3•a2=a6 | D. | (a3)2=a9 |

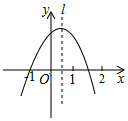 如图,抛物线y=ax2+bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①abc>0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )
如图,抛物线y=ax2+bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①abc>0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )