题目内容
15.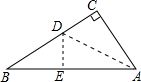 如图,有一个直角三角形纸片,两直角边AC=18cm,BC=24cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则BD=15cm.
如图,有一个直角三角形纸片,两直角边AC=18cm,BC=24cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则BD=15cm.
分析 利用勾股定理列式求出AB=30cm,再根据翻折变换的性质可得AE=AC=18cm,从而得到BE=12cm,设BD=x,则DC=DE=24-x,最后在Rt△DBE中依据勾股定理列方程求解即可.
解答 解:∵∠C=90°,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=30cm.
由翻折的性质可知:∠C=∠DEA=90°,DC=ED,AC=EA=18cm.
BE=AB-AE=30-18=12cm.
设BD=xcm,则DC=ED=(24-x)cm.
在Rt△BDE中由勾股定理得:BD2=EB2+DE2,即x2=122+(24-x)2,
解得:x=15cm.
∴BD=15cm.
故答案为:15cm.
点评 本题主要考查的是翻折的性质、勾股定理的应用,在Rt△BDE中由勾股定理列出关于x的方程是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.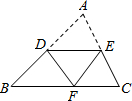 如图,D是AB的中点,将△ABC沿过D的直线折叠,使点A落在BC上的点F处,若∠B=46°,则∠BDF的度数是( )
如图,D是AB的中点,将△ABC沿过D的直线折叠,使点A落在BC上的点F处,若∠B=46°,则∠BDF的度数是( )
 如图,D是AB的中点,将△ABC沿过D的直线折叠,使点A落在BC上的点F处,若∠B=46°,则∠BDF的度数是( )
如图,D是AB的中点,将△ABC沿过D的直线折叠,使点A落在BC上的点F处,若∠B=46°,则∠BDF的度数是( )| A. | 80° | B. | 88° | C. | 92° | D. | 98° |
5. 如图是数学老师给玲玲留的习题,玲玲经过计算得出的正确的结果为( )
如图是数学老师给玲玲留的习题,玲玲经过计算得出的正确的结果为( )
 如图是数学老师给玲玲留的习题,玲玲经过计算得出的正确的结果为( )
如图是数学老师给玲玲留的习题,玲玲经过计算得出的正确的结果为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
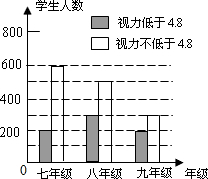 某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图,请根据图中信息解决下列问题:
某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图,请根据图中信息解决下列问题: