题目内容
19.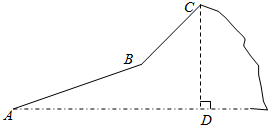 小明春游,登了一座山,地形险峻.由山脚A沿坡角为30°的山坡AB行走480米,到达一个景点B,再由B地沿山坡BC行走360米到达山顶C.如果在山顶C处观测到景点B的俯角为45°,小明在想:山高CD是多少米,你能得出答案吗?(保留$\sqrt{2}$)
小明春游,登了一座山,地形险峻.由山脚A沿坡角为30°的山坡AB行走480米,到达一个景点B,再由B地沿山坡BC行走360米到达山顶C.如果在山顶C处观测到景点B的俯角为45°,小明在想:山高CD是多少米,你能得出答案吗?(保留$\sqrt{2}$)
分析 过B作BE⊥AD于点D,作BF⊥CD于点F,在直角△ABE中,利用三角函数求得BE的长,在直角△BCF中利用三角函数求得CF的长,则CD=BE+CF,据此即可求解.
解答  解:过B作BE⊥AD于点D,作BF⊥CD于点F.
解:过B作BE⊥AD于点D,作BF⊥CD于点F.
在直角△ABE中,∠A=30°,则BE=$\frac{1}{2}$AB=$\frac{1}{2}$×480=240(米);
在直角△BCF中,∠CBF=45°,则CF=BC•sin45°=360×$\frac{\sqrt{2}}{2}$=180$\sqrt{2}$(米).
则CD=CF+DF=CF+BE=240+180$\sqrt{2}$米.
答:山高CD是(240+180$\sqrt{2}$)米.
点评 本题考查仰角的定义,能借助仰角构造直角三角形并解直角三角形是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
9.在$-2,\sqrt{4},\sqrt{2},3.14,\root{3}{-27},π$这6个数中,无理数共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
4.下列结论中,正确的是( )
| A. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | B. | 若a>b,则a2>b2 | C. | 若a>b,则1-a<1-b | D. | 若a>b,ac2>bc2 |
11. 下列四幅图案中,能通过轴对称由图案1得到的是( )
下列四幅图案中,能通过轴对称由图案1得到的是( )
 下列四幅图案中,能通过轴对称由图案1得到的是( )
下列四幅图案中,能通过轴对称由图案1得到的是( )| A. |  | B. |  | C. |  | D. |  |
8.下列运算中,正确的是( )
| A. | x2+x3=x5 | B. | (x2)3=x6 | C. | 2x3÷x2=x | D. | 2x-1=$\frac{1}{2x}$ |
 已知线段AD上有B、C两点,说出图中总共有哪几条线段.
已知线段AD上有B、C两点,说出图中总共有哪几条线段.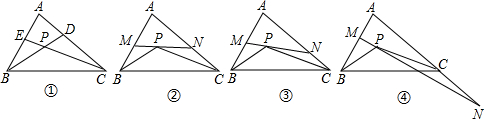
 如图,已知DE∥BC,∠1=∠2,那么∠B与∠C相等吗?为什么?
如图,已知DE∥BC,∠1=∠2,那么∠B与∠C相等吗?为什么?