题目内容
如图，在△OAB中，OA=OB=2，∠OAE=30°，⊙O切AB于E，且分别交OA、OB于C、D，求图中阴影部分的面积．
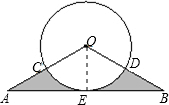解：连接OE．∵⊙O切AB于E，∴OE⊥AB，∴∠OEA=90度．
在Rt△OEA中，∠OAE=30°，OA=2
∴OE=
OA=1，∠AOE=60°．∴AE=
=
．∵OE⊥AB，OB=OA，
∴BE=2AE=2
，∠AOB=2∠OBE=120°．∴S阴影=S△OAB-S扇形OCD=
AB•OE-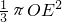
=-
．分析：由图易知：阴影部分的面积=三角形的面积-扇形的面积．所以要求阴影部分的面积，就要通过解直角三角形，求得∠AOB的度数以及圆的半径OC的长．可连接OE，在构建的Rt△AOE中，求得上述值．
点评：本题主要考查了解直角三角形的应用和扇形的面积公式的计算方法．
练习册系列答案
口算能手系列答案
相关题目
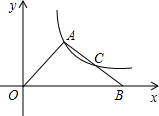（2012•泸州）如图，在△OAB中，C是AB的中点，反比例函数y=
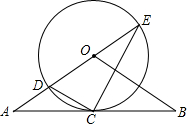如图，在△OAB中，OA=OB，以点O为圆心的⊙0经过AB的中点C，直线AO与⊙0相交于点D、E，连接CD、CE．
如图，在△OAB中，C是AB的中点，反比例函数y=
如图，在△OAB中，∠B=90°，∠BOA=30°，OA=4，将△OAB绕点O按逆时针方向旋转至△OA′B′，C点的坐标为（0，4）．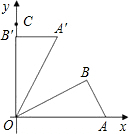
（创新学习）如图，在△OAB中，∠B=90°，∠BOA=30°，OA=4，将△OAB绕点O按逆时针方向旋转至△OA′B′，C点的坐标为（0，4）．