题目内容
9.如图,已知AB∥CD,猜想图(1)、图(2)、图(3)中,∠B,∠E,∠D之间有什么关系?请用等式表示出它们的关系,并证明其中的一个等式.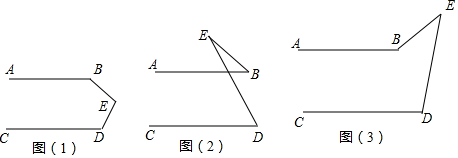
分析 图(1)中,∠B+∠BED+∠D=360°,根据两直线平行,同旁内角互补进行推导即可;图(2)中,∠B+∠E=∠D,根据两直线平行,同位角相等,以及三角形外角性质进行推导即可;图(3)中,∠ABE-∠E=∠D,根据两直线平行,同位角相等,以及三角形外角性质进行推导即可.
解答 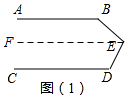 解:图(1)中,∠B+∠BED+∠D=360°.
解:图(1)中,∠B+∠BED+∠D=360°.
证明:过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠B+∠BEF=180°,∠D+∠DEF=180°,
∴∠B+∠BED+∠D=180°+180°=360°.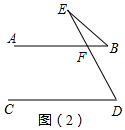
图(2)中,∠B+∠E=∠D.
证明:∵AB∥CD,
∴∠D=∠AFE,
∵∠AFE是△BEF的外角,
∴∠B+∠E=∠AFE,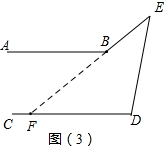
∴∠B+∠E=∠D.
图(3)中,∠ABE-∠E=∠D.
证明:∵AB∥CD,
∴∠ABE=∠CFE,
∵∠CFE是△DEF的外角,
∴∠CFE-∠E=∠D,
∴∠ABE-∠E=∠D.
点评 本题主要考查了平行线的性质以及三角形外角性质的运用,解决问题的关键是作辅助线,解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
19.分式$\frac{35{a}^{2}{b}^{2}}{15{a}^{3}bc}$约分的结果是( )
| A. | $\frac{7b}{3a}$ | B. | $\frac{7b}{3ac}$ | C. | $\frac{3a}{7b}$ | D. | $\frac{3ac}{7b}$ |
4.下列不能用平方差公式计算的是( )
| A. | (-5-a)(a-5) | B. | (-2a+3b)(3b+2a) | C. | (a+b+c)(a-b+c) | D. | (a-b-c)(-a+b+c) |
18.下列计算正确的是( )
| A. | (-14)-(+5)=-9 | B. | 0-(-3)=0+(-3) | C. | (-3)×(-3)=-6 | D. | (-18)÷(-$\frac{2}{3}$)=27 |
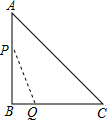 如图,在△ABC中,∠B=90°,AB=BC=4,动点P从点A出发沿A→B→C运动,动点Q从点B出发沿B→C→A运动.如果P、Q两点同时出发,速度均为1个单位/秒.设出发时间为x秒(0≤x≤8),记△PBQ的面积y1的函数图象为T.若直线y2=x+b与T只有一个交点,则b的取值范围为b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8<b<0或b=$\frac{1}{2}$.
如图,在△ABC中,∠B=90°,AB=BC=4,动点P从点A出发沿A→B→C运动,动点Q从点B出发沿B→C→A运动.如果P、Q两点同时出发,速度均为1个单位/秒.设出发时间为x秒(0≤x≤8),记△PBQ的面积y1的函数图象为T.若直线y2=x+b与T只有一个交点,则b的取值范围为b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8<b<0或b=$\frac{1}{2}$.