题目内容
20.若a=$\sqrt{2}$-3,求$2(a-\sqrt{2})+(a+\sqrt{2})-a(a-3)+4$的值.分析 先把代数式化简,再进一步代入求得数值即可.
解答 解:原式=2a-2$\sqrt{2}$+a+$\sqrt{2}$-a2+3a+4
=-a2+6a+4-2$\sqrt{2}$
当a=$\sqrt{2}$-3时,
原式=-($\sqrt{2}$-3)2+6($\sqrt{2}$-3)+4-2$\sqrt{2}$
=-(11-6$\sqrt{2}$)+6$\sqrt{2}$-18+4-2$\sqrt{2}$
=-11+6$\sqrt{2}$+6$\sqrt{2}$-18+4-2$\sqrt{2}$
=10$\sqrt{2}$-25.
点评 此题考查二次根式的化简求值,掌握计算的方法是解决问题的关键.

练习册系列答案
相关题目
8.下列一组数:-8、2.7、-3$\frac{1}{2}$、$\frac{π}{2}$、0.66666…、0、2、0.080080008…,其中是有理数的个数是( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
15.下面计算正确的是( )
| A. | -(-3)2=32 | B. | ${(-3)^2}×({\frac{2}{3}})=-6$ | C. | -5-2=-3 | D. | -(-0.2)2=0.22 |
9.点P(2,3)关于原点的对称点的坐标是( )
| A. | (2,3 ) | B. | (-2,-3) | C. | (-2,3) | D. | (-3,2) |
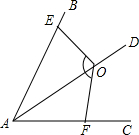 如图,∠BAC=60°,O是∠BAC平分线上的一点,点E、F分别在AB、AC上,若∠EOF=120°,求证:OE=OF.
如图,∠BAC=60°,O是∠BAC平分线上的一点,点E、F分别在AB、AC上,若∠EOF=120°,求证:OE=OF.