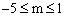题目内容
如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0, 3)。
(1)求抛物线的解析式;
(2)若点P为抛物 线在第二象限上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
线在第二象限上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由。
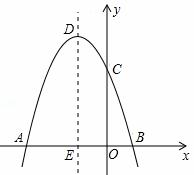
1)∵抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),
∴可设抛物线的解析式为: ,
,
将C点坐标(0, 3)代入,得: ,解得
,解得  。
。
∴抛物线的解析式为: ,即
,即 。
。


∴PN=PE﹣NE=(
 )﹣(
)﹣( )=﹣x2﹣3x。
)=﹣x2﹣3x。
∵S△P AC=S△PAN+S△PCN,
AC=S△PAN+S△PCN,
∴ 。
。
∴当x=  时,S有最大值
时,S有最大值 ,此时点P的坐标为(
,此时点P的坐标为( ,
, )。
)。
(3)在y轴上存在点M,能够使得△ADE是等腰直角三角形。理由如下:
∵ ,∴顶点D的坐标为(﹣1, 4)。
,∴顶点D的坐标为(﹣1, 4)。


【考点】二次函数综合题,待定系数法的应用,曲线上点的坐标与方程的关系,由实际问题列函数关系式,二次函数的性质,线段垂直平分线的性质,勾股定理和逆定理。


练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 (1)此次抽样调查中,共调查了 名学生;
(1)此次抽样调查中,共调查了 名学生;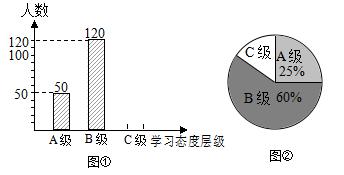
 向B地,
向B地, 甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.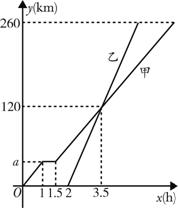


 数表达式
数表达式 ,并写出相应
,并写出相应 抛
抛 与运行的水平距离x(m)满足关系式
与运行的水平距离x(m)满足关系式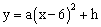 。已知球网与O点
。已知球网与O点 的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。 二次函数中二次项系数a的最大值。
二次函数中二次项系数a的最大值。
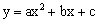 的图象如图所示,反比例函数
的图象如图所示,反比例函数 与一次函数
与一次函数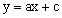 在同一平面直角坐标系中的大致图象是【 】
在同一平面直角坐标系中的大致图象是【 】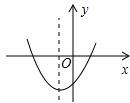
 B.
B.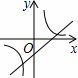

 C.
C. D.
D.
 ,则反比例函数且反比例函数
,则反比例函数且反比例函数 的图象在每个象限内y随x的增大而增大,那么反比例函数的关系式为【 】
的图象在每个象限内y随x的增大而增大,那么反比例函数的关系式为【 】 B.
B.  C.
C.  D.
D. 

 cm,则
cm,则 四边形ABCD的面积是 cm2。
四边形ABCD的面积是 cm2。
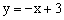 沿y轴方向平移m个单位后,与直线
沿y轴方向平移m个单位后,与直线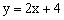 的交点在第二象限,则m的取值范围是【 】
的交点在第二象限,则m的取值范围是【 】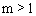 B.
B.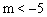 C.
C.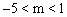 D.
D.