题目内容
如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,则线段EF的长是 cm.
【答案】分析:过O点作OH⊥EF于H,连OF,根据垂径定理得EH=FH,在Rt△AOH中,AO=AD+OD=3+5=8,∠A=30°,利用含30度的直角三角形三边的关系可得到OH= OA=4,再利用勾股定理计算出HF,由EF=2HF得到答案.
OA=4,再利用勾股定理计算出HF,由EF=2HF得到答案.
解答:解:过O点作OH⊥EF于H,连OF,如图
则EH=FH,
在Rt△AOH中,AO=AD+OD=3+5=8,∠A=30°,
则OH= OA=4,
OA=4,
在Rt△OHF中,OH=4,OF=5,
则HF= =3,
=3,
则EF=2HF=6cm.
故答案为6.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了含30度的直角三角形三边的关系以及勾股定理.
 OA=4,再利用勾股定理计算出HF,由EF=2HF得到答案.
OA=4,再利用勾股定理计算出HF,由EF=2HF得到答案.解答:解:过O点作OH⊥EF于H,连OF,如图

则EH=FH,
在Rt△AOH中,AO=AD+OD=3+5=8,∠A=30°,
则OH=
 OA=4,
OA=4,在Rt△OHF中,OH=4,OF=5,
则HF=
 =3,
=3,则EF=2HF=6cm.
故答案为6.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了含30度的直角三角形三边的关系以及勾股定理.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
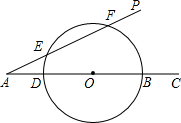 已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长. 已知:如图,∠PAC=30°,在射线AC上顺次截取AD=2cm,DB=6cm,以DB为直径作⊙O交射线AP于E、F两点,又OM⊥AP于M.求OM及EF的长.
已知:如图,∠PAC=30°,在射线AC上顺次截取AD=2cm,DB=6cm,以DB为直径作⊙O交射线AP于E、F两点,又OM⊥AP于M.求OM及EF的长.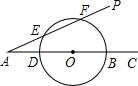 (2012•辽阳)如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,则线段EF的长是
(2012•辽阳)如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,则线段EF的长是
