题目内容
 已知:如图,∠PAC=30°,在射线AC上顺次截取AD=2cm,DB=6cm,以DB为直径作⊙O交射线AP于E、F两点,又OM⊥AP于M.求OM及EF的长.
已知:如图,∠PAC=30°,在射线AC上顺次截取AD=2cm,DB=6cm,以DB为直径作⊙O交射线AP于E、F两点,又OM⊥AP于M.求OM及EF的长.
分析:连接OF,由DB=6cm,求得OD的长,则可求得OA的长,由OM⊥AP,∠PAC=30°,即可求得OM的长,然后在Rt△OMF中,利用勾股定理即可求得FM的长,又由垂径定理,即可求得EF的长.
解答: 解:连接OF,
解:连接OF,
∵DB=6cm,
∴OD=3cm,
∴AO=AD+OD=2+3=5cm,
∵∠PAC=30°,OM⊥AP,
∴在Rt△AOM中,OM=
AO=
×5=
cm
∵OM⊥EF,
∴EM=MF,
∵MF=
=
=
cm
∴EF=
cm.
 解:连接OF,
解:连接OF,∵DB=6cm,
∴OD=3cm,
∴AO=AD+OD=2+3=5cm,
∵∠PAC=30°,OM⊥AP,
∴在Rt△AOM中,OM=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∵OM⊥EF,
∴EM=MF,
∵MF=
| OF2-OM2 |
32-(
|
| ||
| 2 |
∴EF=
| 11 |
点评:此题考查了直角三角形中30°角的性质、勾股定理、垂径定理等几个知识点.此题难度不大,解题的关键是注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
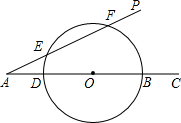 已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.

